抛物线法
抛物线法
充分利用已试验的结果来进行再试验的一种单因素优选方法。当一个实际决策问题存在最大值,且能够依据试验结果近似求出其函数关系时,就有可能用抛物线法更快找到最佳点。抛物线法的具体作法是: (1) 对某因素在其变化区间 〔x1,x3〕 的端点x1处和x3处进行试验,以取得两个结果数据。(2) 接着在 〔x1,x3〕 区间上任意一点x2处进行试验以取得数据。(3) 比较以上三处的试验结果数据y1、y2、y3,当y2比y1和y3都大时,就可过y1、y2、y3三点作 一条抛物线。(4) 以该抛物线顶点对应的x0处作为第四次试验点,试验结果可作为最优方案的结果。用图形可表示如下:
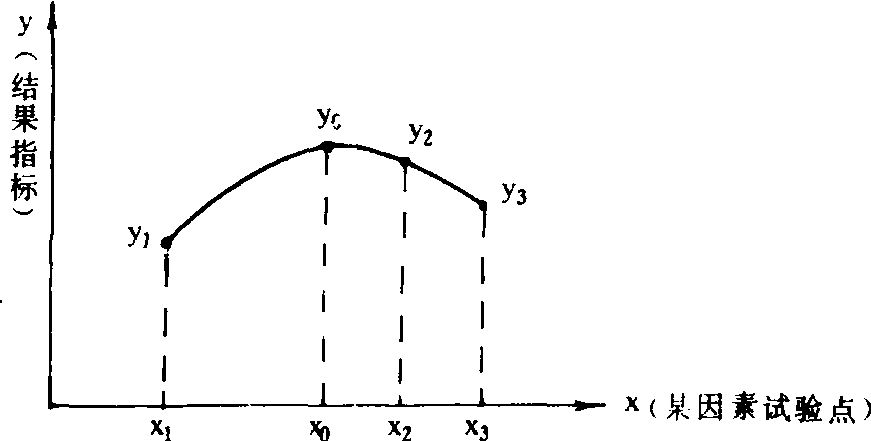
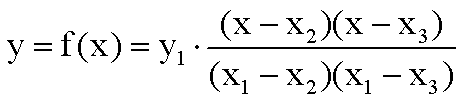
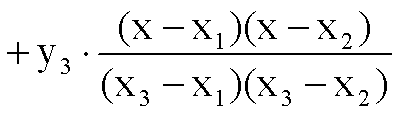
并且抛物线在x0处的最大值为:
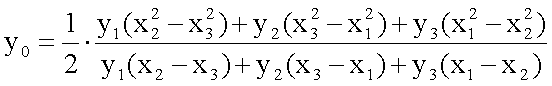
☚ 对分法 双因素优选法 ☛
- 海上三山图是什么意思
- 海上丝绸之路是什么意思
- 海上丝绸之路是什么意思
- 海上丝绸之路是什么意思
- 海上丝绸之路》是什么意思
- 海上丝路是什么意思
- 海上丝路是什么意思
- 海上之盟是什么意思
- 海上之盟是什么意思
- 海上之盟是什么意思
- 海上之盟是什么意思
- 海上之盟是什么意思
- 海上之盟是什么意思
- 海上之盟是什么意思
- 海上事故调查是什么意思
- 海上交通线是什么意思
- 海上人工岛建设是什么意思
- 海上侦察是什么意思
- 海上保交战是什么意思
- 海上保交战是什么意思
- 海上保险是什么意思
- 海上保险是什么意思
- 海上保险是什么意思
- 海上保险是什么意思
- 海上保险是什么意思
- 海上保险是什么意思
- 海上保险是什么意思
- 海上保险单是什么意思
- 海上保险合同是什么意思
- 海上保险合同是什么意思
- 海上保险合同是什么意思
- 海上保险合同是什么意思
- 海上保险合同是什么意思
- 海上保险合同是什么意思
- 海上保险合同是什么意思
- 海上保险学是什么意思
- 海上保险法是什么意思
- 海上倾废是什么意思
- 海上养殖工程是什么意思
- 海上劳工是什么意思
- 海上医宗心领是什么意思
- 海上医宗心领全帙是什么意思
- 海上医宗心领全帙是什么意思
- 海上十闻人是什么意思
- 海上反封锁是什么意思
- 海上四任精品是什么意思
- 海上城市是什么意思
- 海上城市是什么意思
- 海上城市是什么意思
- 海上墨林是什么意思
- 海上安装是什么意思
- 海上封锁是什么意思
- 海上尘天影是什么意思
- 海上尘天影是什么意思
- 海上巡逻是什么意思
- 海上工厂是什么意思
- 海上布雷是什么意思
- 海上平台是什么意思
- 海上扫雷是什么意思
- 海上护航是什么意思