弦的振动xian de zhendong

物体振动的理想模型之一。理想的振动弦系指具有一定长度、一定质量（横截面与质量线密度均为常数）的柔软（无刚性）的细丝或细绳拉紧并两端固定，以张力作为弹性恢复力进行振动的弹性体。当用手指轻弹弦即可激起弦的横振动，在小振幅情况下，弦上的张力T是均匀的，为一常数，略去重力，不计一切阻力，称为弦的自由振动。由牛顿第二定律可以得到弦上坐标为的P点的振动动力学程，式中y是点P垂直于弦的方向的位移，单位为米，t是时间，单位为秒，v是波动在弦上传播的速度，单位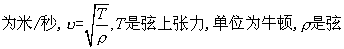的质量线密度，单位为千克/米。当弦长为l时，用分离变量法（或叫驻波法）求得波动方程满足边界条件yx_＝0＝0,yx=l=0的解，即弦上各点振动位移是时间的余弦函数（或正弦函数）的线性叠加。弦振动的振动频率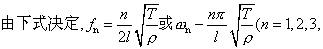…)，即对于两端固定的弦，振动频率具有一系列特定的数值，fn=f1,f₂,f₃，…。且仅由弦本身的固有力学参量(l,T和ρ)决定，故称f_n为弦的固有振动频率。注意，谐振子仅有一个固有频率，而弦的固有频率有n个，且必须满足fn=n/2_l，以n=1,2,3，…等次序离散变化，常称弦的这种固有频率为简正频率。n=1,f₁＝v/2l为弦的最低固有频率，称为弦的基频，n>1的各次频率称为泛频，如n=2,f₂＝v/l称为第一次泛频（相应地在声学中叫第一次泛音）。由于弦振动的各次泛频均为基频的整数倍，因此常称具有这种简单关系的固有频率为谐频。称基频为第一谐频（相应地在声学中叫基波和基音）,f₂为第二谐频(相应地在声学中叫2次谐波和2次谐音)。注意：基频n倍的音是第(n-1)次泛音，n次谐音。弦作自由振动时，一般同时有许多简正频率在振动，这一系列简正频率f_n对应的振动位移为yn=Bnsinnπ/lxcos2πfn_t-ᵠn。此式称为弦的频率为fn的第n次简正振动方式。其中ᵠn, B_n是第n次振动方式相应的由初始条件决定的常数。这种简正振动方式在弦上表现为波腹、波节固定分布的驻波振动形式。n次简正振动方式在弦上形成n次谐波，n次谐波连同弦两端固定无位移的节点一起共有(n+1)个节点，有n个波腹。每一个简正振动方式都是波动方程的一个特解。所以某一时刻弦振动是各种振动方式的叠加。因此波动方程的一般解为所有简正振动方式的线性迭加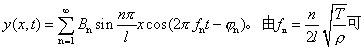：知，改变长度l或张力T或ρ都可以改变弦振动的固有频率，由此可改变弦乐器的音调和音色。弦乐器如胡琴、琵琶、提琴等都是根据弦的振动原理制成的。