广义最小平方法Generalized Least Square Method
适用于存在异方差和序列相关条件情况时的最小平方法。是普通最小平方法的引伸。普通最小平方法要求研究对象的真实模型具备同方差性和序列无关性条件,但实际上许多事物不具备这种条件。补救的办法是变换原模型中的变量,消除异方差和序列相关后再用普通最小平方法估计参数。设有回归方程式模型为:
Yi=β0+β1X1i+β2X2i+ui,i=1,2,…,N ……… (1)
其中,u1,u2,…,uN为互不相关的随机干扰项,均值为0,标准差为σ1,σ2,…,σN(σ1≠σ2≠-≠σN,即干扰项具有异方差性)。将 (1) 式除以σi,得: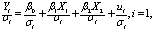
![]()
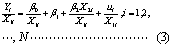
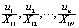
- 孙玄常是什么意思
- 孙玉国是什么意思
- 孙玉声是什么意思
- 孙玉平是什么意思
- 孙玉庭自记年谱是什么意思
- 孙玉成是什么意思
- 孙玉敏是什么意思
- 孙玉清是什么意思
- 孙玉田是什么意思
- 孙玉石是什么意思
- 孙玉章是什么意思
- 孙玉胜是什么意思
- 孙玉香是什么意思
- 孙玘是什么意思
- 孙玚是什么意思
- 孙玮芒是什么意思
- 孙玲是什么意思
- 孙玲香是什么意思
- 孙玺凤是什么意思
- 孙球是什么意思
- 孙理是什么意思
- 孙理甫是什么意思
- 孙琛是什么意思
- 孙琦是什么意思
- 孙琬是什么意思
- 孙琮是什么意思
- 孙琮画像石墓是什么意思
- 孙琳是什么意思
- 孙琼是什么意思
- 孙瑀是什么意思
- 孙瑛是什么意思
- 孙瑜是什么意思
- 孙瑜传是什么意思
- 孙瑞是什么意思
- 孙瑞剑铭是什么意思
- 孙瑞林是什么意思
- 孙瑞璋是什么意思
- 孙瑞璜是什么意思
- 孙瑞符是什么意思
- 孙瑞芹是什么意思
- 孙瑶英是什么意思
- 孙瑾是什么意思
- 孙璋是什么意思
- 孙璞是什么意思
- 孙璧媃是什么意思
- 孙璧文是什么意思
- 孙瓘等伪造印信案是什么意思
- 孙生乞道是什么意思
- 孙生禄是什么意思
- 孙用是什么意思
- 孙用和是什么意思
- 孙用康是什么意思
- 孙甫亭是什么意思
- 孙甫舂粟案是什么意思
- 孙田公路是什么意思
- 孙男是什么意思
- 孙男个女是什么意思
- 孙男娣女是什么意思
- 孙男嫡女是什么意思
- 孙男子是什么意思