平面与球面的关系
平面与球面的关系pingmian yu qiumian de guanxi
平面与球面的相关位置有三种,即相离、相切、相交。平面xcosα+ ycosβ+zcosγ=p与球面 (x-x0)2+(y-y0)2+(z-z0)2=r2相离、要切、相交的充要条件是d>r,d=r,d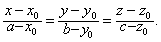
☚ 直线与球面的关系 两球面的关系 ☛
- 毫欧计是什么意思
- 毫毛是什么意思
- 毫毛不拔,将成斧柯是什么意思
- 毫毛不犯是什么意思
- 毫毛斧柯是什么意思
- 毫毛 糟粕是什么意思
- 毫毛虽小,视之可察;太山虽大,背之不见是什么意思
- 毫毫是什么意思
- 毫毫子是什么意思
- 毫泥是什么意思
- 毫洋是什么意思
- 毫洋券是什么意思
- 毫添颊上是什么意思
- 毫烧是什么意思
- 毫燥是什么意思
- 毫生馆是什么意思
- 毫相是什么意思
- 毫眉是什么意思
- 毫秒爆破是什么意思
- 毫秒雷管是什么意思
- 毫穎是什么意思
- 毫窍是什么意思
- 毫端是什么意思
- 毫端分马颊,墨点辨蛾眉。是什么意思
- 毫端妙理是什么意思
- 毫端阁是什么意思
- 毫管是什么意思
- 毫米是什么意思
- 毫米汞柱是什么意思
- 毫米波是什么意思
- 毫米波制导是什么意思
- 毫米波制导炮弹是什么意思
- 毫米波无线通信是什么意思
- 毫米波波导通信是什么意思
- 毫米波通信是什么意思
- 毫米波通信设备是什么意思
- 毫米波雷达是什么意思
- 毫系是什么意思
- 毫素是什么意思
- 毫纤是什么意思
- 毫罗溪铁路大桥是什么意思
- 毫翰是什么意思
- 毫芒是什么意思
- 毫谷是什么意思
- 毫釐是什么意思
- 毫針是什么意思
- 毫銛是什么意思
- 毫錐是什么意思
- 毫针是什么意思
- 毫针刺法是什么意思
- 毫针疗法是什么意思
- 毫铢是什么意思
- 毫铦是什么意思
- 毫锥是什么意思
- 毫露是什么意思
- 毫颖是什么意思
- 毫髮是什么意思
- 毫麻是什么意思
- 毫黍是什么意思
- 毬是什么意思