对偶单纯形法

求解线性规划模型单纯形法的对称。一种用对偶理论来指导求解线性规划模型的方法。对偶单纯形方法，在理解线性规划模型单纯形解法 （见单纯形法） 的基础上，可按下述步骤进行： 第一步：模型标准化，填充初始单纯形表。为了使用这种算法，填充的初始表中，必须满足所有C_j-Z_j≤0而b列允许存在有负分量； 第二步： 选择b_i<0分量中绝对值最大的分量所在行为主行、对应这个行的基变量就是出基变量，并可作标记*; 第三步： 对主行i*中具有负元素的那些列，由下式计算比值：

选择最小比值min{Φj}所在列为主列，对应这个列的非基变量就是进基变量； 第四步： 对确定好的进基变量和出基变量进行代换，按一般单纯形表运算的方法，进行迭代运算，得到新的单纯形表； 第五步： 检查b列，如果所有bi≥0，停止迭代过程，写出最优解。否则，返回第二步。
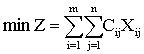
对偶单纯形法是1954年由莱姆凯创立的，这种方法可以简化某些线性规划模型的求解，特别是在线性规划模型的实际经济应用中，它是进行灵敏分析的一个重要工具。