定积分的近似计算法
定积分的近似计算法dingjifen de jinsijisuan fa
若定积分 f (x)d x的被积函数f (z)不具备应用微积分基本公式的条件,或虽具备了上述条件但计算过于繁杂,则需要根据精度要求作定积分的近似计算. 常用的定积分近似计算方法有梯形法,抛物线法等. 公式如下:
f (x)d x的被积函数f (z)不具备应用微积分基本公式的条件,或虽具备了上述条件但计算过于繁杂,则需要根据精度要求作定积分的近似计算. 常用的定积分近似计算方法有梯形法,抛物线法等. 公式如下:
梯形法
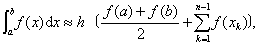
其中
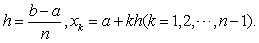
误差不超过
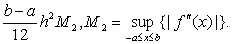
抛物线法 (辛卜森公式)
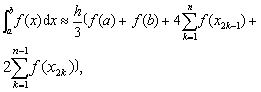
其中
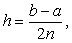 x1=a+kh (k=1,2,…,2n-1). 误差不超过
x1=a+kh (k=1,2,…,2n-1). 误差不超过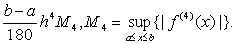
在等分的小区间个数相等的情况下,抛物线法的结果比梯形法精确。
例 利用梯形法计算
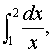 精确到0.01.
精确到0.01.解 对于f (x)=1/x,
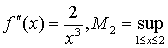
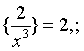 因此,误差不超过
因此,误差不超过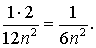
要使误差小于0. 01,只需解不等式
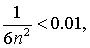 取其解集中的最小值n=5即可.
取其解集中的最小值n=5即可.误差小于
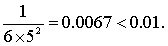
计算函数值时,要设法使新得到的四舍五入的误差之和小于0. 003.
x0=1 y0=1.000
x1=1.2 y1=0. 833
x2=1.4 y2=0. 714
x3=1.6 y3=0. 625
x4=1.8 y4=0. 556
x5=2.0 y5=0. 500
因此,
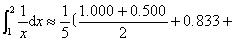 0.714+0.625+0.556]=0. 696.
0.714+0.625+0.556]=0. 696.☚ 变力所作的功 电子计算机 ☛
- 云表师馆是什么意思
- 云表歌云遏是什么意思
- 云衫是什么意思
- 云衫衫是什么意思
- 云衬是什么意思
- 云衲是什么意思
- 云袍是什么意思
- 云被歌声摇动,酒被诗情掇送。是什么意思
- 云装是什么意思
- 云裘是什么意思
- 云裳是什么意思
- 云裾是什么意思
- 云西是什么意思
- 云覆银塘,风吹野葛,是什么意思
- 云覆雨施是什么意思
- 云观是什么意思
- 云觥是什么意思
- 云计算是什么意思
- 云讯是什么意思
- 云记是什么意思
- 云诏是什么意思
- 云话儿是什么意思
- 云课堂是什么意思
- 云谁之思?西方美人。是什么意思
- 云谊是什么意思
- 云谓字是什么意思
- 云谣是什么意思
- 云谣集是什么意思
- 云谣集杂曲子是什么意思
- 云谣集杂曲子一卷是什么意思
- 云谣集杂曲子三十首是什么意思
- 云谲是什么意思
- 云谲波诡是什么意思
- 云谲波诡波谲云诡是什么意思
- 云谲波诡,风狂雨横是什么意思
- 云谲波诡;风狂雨横是什么意思
- 云谷是什么意思
- 云谷卧余是什么意思
- 云谷叟是什么意思
- 云谷子是什么意思
- 云谷寺景区是什么意思
- 云谷山庄是什么意思
- 云谷早行图是什么意思
- 云谷杂记是什么意思
- 云谷老人是什么意思
- 云谷诗馀是什么意思
- 云谷轩是什么意思
- 云谿是什么意思
- 云谿乐府是什么意思
- 云豆是什么意思
- 云豆卷是什么意思
- 云豹是什么意思
- 云貌是什么意思
- 云贞是什么意思
- 云贵会馆是什么意思
- 云贵总督是什么意思
- 云贵音乐乐种面面观是什么意思
- 云贵音乐文化区的风格特点是什么意思
- 云贵音乐文化形成与发展的历史背景是什么意思
- 云贵高原是什么意思