定积分
第一,当知西人所谓点、线、面皆不能无体。……
第二,当知体可变为面,面可变为线。……
第三,当知诸乘方有线、面、体循环之理。一乘方为面(即平方),二乘方为体(即立方);三乘方为线(线即中法立天元之元,西法借根方之方也),四乘方复为面,五乘方复为体;六乘方复为线,推之至于无穷,其为线、面、体三者循环无已。……
第四,当知诸乘方皆可变为面,并皆可变为线①。观第二条其理自明。
第五,当知平、立尖锥之形。……
第六,当知诸乘方皆有尖锥。三乘以上尖锥之底皆方,唯上四面不作平体而成凹形。乘愈多则凹愈甚。……
第七,当知诸尖锥有积叠之理。元数(即立天元之元)起于丝发而递增之,而叠之则成平尖锥;一定之元数叠之则成平方,上少下多之元数叠之则成平尖锥(第一层一,第二层二,第三层三)。平方数起于丝发而渐增之而叠之,则成立尖锥;一定之平方叠之则成立方,上少下多之平方叠之则成立尖锥(第一层一,第二层四,第三层九)。立方数起于丝发而渐增之变为面(体可变面,说见前),而叠之则成三乘尖锥(第一层一,第二层八,第三层二十九)。三乘方数起于丝发而渐增之变为面,而叠之则成四乘尖锥(第一层一,第二层十六,第三层八十一)。从此递推可至无穷,然则多一乘之尖锥皆少一乘方,渐增渐叠而成也②。
第八,当知诸尖锥之算法。以高乘底为实,本乘方数加一为法,除之得尖锥积③。……
第九,当知二乘以上尖锥,其所叠之面皆可变为线④。面变为线,则诸尖锥皆成平体而曲其边。正则曲二边,偏则曲一边。乘益多则曲益甚。
第十,当知诸尖锥既为平面则可并为一尖锥。诸尖锥既为平面,则无棱角,故可并。法:先立一尖锥,次以一尖锥凸其一面,如先立尖锥之曲线,则两尖锥便可合而为一矣。诸尖锥皆以此法并之⑤。……
[注]①此谓若x为正数,n为正整数,则xn可用一个平面积表示,亦可用一条直线段表示。②此谓:若0≤x≤h,则表示xn的平面积积叠成一尖锥体。③此谓:由平面积axn积叠而成的尖锥体,高为h,底面积为ahn,则其体积为。它相当于定积分。④此谓axn可以用一条直线段表定积分。
【评】以上十条命题是李善兰尖锥术的基本理论,其中有的命题含有定积分思想,虽未十分严谨,在西方产生并发展起来的微积分学传入中国之前,这是难能可贵的。
方内函圆,方圆之较即诸乘方之合尖锥也①。起再乘,次四乘,次六,次八,次十,至于无穷,其数有隅而无奇,一阴一阳之道也。再乘尖锥之底,二分半径之一也;以其馀四分之,为四乘尖锥之底;又以其馀六分之,为六乘尖锥之底;其尖锥若干乘,则底亦若干分之一焉;如是至于无尽,生生不穷之道也②。[此下图解,略]既得诸尖锥之底,依前第八条法,以求其积③。既得诸积,四因之,以减外大方积,便见大圆真积也④。
[注]①此为通过求出圆与其外切正方形之间的面积解决圆面积问题。先考虑其四分之一,是为诸乘方之合尖锥。②诸锥底分别为,……,其中r是圆半径。③依上第八条,诸尖锥积为④圆面积4r2-4……)若令r=1,便为
【评】此为将尖锥术用于圆面积,得到圆面积的级数展开式。此外,李善兰还将尖锥求积术用于求对数函数的幂级数展开(见《对数探源》)。
第二,当知体可变为面,面可变为线。……
第三,当知诸乘方有线、面、体循环之理。一乘方为面(即平方),二乘方为体(即立方);三乘方为线(线即中法立天元之元,西法借根方之方也),四乘方复为面,五乘方复为体;六乘方复为线,推之至于无穷,其为线、面、体三者循环无已。……
第四,当知诸乘方皆可变为面,并皆可变为线①。观第二条其理自明。
第五,当知平、立尖锥之形。……
第六,当知诸乘方皆有尖锥。三乘以上尖锥之底皆方,唯上四面不作平体而成凹形。乘愈多则凹愈甚。……
第七,当知诸尖锥有积叠之理。元数(即立天元之元)起于丝发而递增之,而叠之则成平尖锥;一定之元数叠之则成平方,上少下多之元数叠之则成平尖锥(第一层一,第二层二,第三层三)。平方数起于丝发而渐增之而叠之,则成立尖锥;一定之平方叠之则成立方,上少下多之平方叠之则成立尖锥(第一层一,第二层四,第三层九)。立方数起于丝发而渐增之变为面(体可变面,说见前),而叠之则成三乘尖锥(第一层一,第二层八,第三层二十九)。三乘方数起于丝发而渐增之变为面,而叠之则成四乘尖锥(第一层一,第二层十六,第三层八十一)。从此递推可至无穷,然则多一乘之尖锥皆少一乘方,渐增渐叠而成也②。
第八,当知诸尖锥之算法。以高乘底为实,本乘方数加一为法,除之得尖锥积③。……
第九,当知二乘以上尖锥,其所叠之面皆可变为线④。面变为线,则诸尖锥皆成平体而曲其边。正则曲二边,偏则曲一边。乘益多则曲益甚。
第十,当知诸尖锥既为平面则可并为一尖锥。诸尖锥既为平面,则无棱角,故可并。法:先立一尖锥,次以一尖锥凸其一面,如先立尖锥之曲线,则两尖锥便可合而为一矣。诸尖锥皆以此法并之⑤。……
清·李善兰《方圆阐幽》(见《则古昔斋算学》)
[注]①此谓若x为正数,n为正整数,则xn可用一个平面积表示,亦可用一条直线段表示。②此谓:若0≤x≤h,则表示xn的平面积积叠成一尖锥体。③此谓:由平面积axn积叠而成的尖锥体,高为h,底面积为ahn,则其体积为。它相当于定积分。④此谓axn可以用一条直线段表定积分。
【评】以上十条命题是李善兰尖锥术的基本理论,其中有的命题含有定积分思想,虽未十分严谨,在西方产生并发展起来的微积分学传入中国之前,这是难能可贵的。
方内函圆,方圆之较即诸乘方之合尖锥也①。起再乘,次四乘,次六,次八,次十,至于无穷,其数有隅而无奇,一阴一阳之道也。再乘尖锥之底,二分半径之一也;以其馀四分之,为四乘尖锥之底;又以其馀六分之,为六乘尖锥之底;其尖锥若干乘,则底亦若干分之一焉;如是至于无尽,生生不穷之道也②。[此下图解,略]既得诸尖锥之底,依前第八条法,以求其积③。既得诸积,四因之,以减外大方积,便见大圆真积也④。
清·李善兰《方圆阐幽》(《则古昔斋算学》)
[注]①此为通过求出圆与其外切正方形之间的面积解决圆面积问题。先考虑其四分之一,是为诸乘方之合尖锥。②诸锥底分别为,……,其中r是圆半径。③依上第八条,诸尖锥积为④圆面积4r2-4……)若令r=1,便为
【评】此为将尖锥术用于圆面积,得到圆面积的级数展开式。此外,李善兰还将尖锥求积术用于求对数函数的幂级数展开(见《对数探源》)。
定积分
定积分dingjffen
是积分学的基本概念之一. 设函数f (x)在区间 [a,b]上有定义,用分点
a = x0
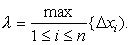 在每一个小区间[xi-1,xi]上任取一点ξi,并且作和
在每一个小区间[xi-1,xi]上任取一点ξi,并且作和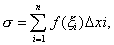 这个和称为函数f (x)在区间 [a,b ]上的积分和.若当λ→0时,不管区间[a,b]的分法如何,也不管ξ的取法如何,和数σ存在极限I,即
这个和称为函数f (x)在区间 [a,b ]上的积分和.若当λ→0时,不管区间[a,b]的分法如何,也不管ξ的取法如何,和数σ存在极限I,即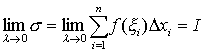
则称极限值I为函数f (x)在区间[a,b]上的定积分记作
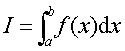
定积分的定义也可用ε—δ语言来表述.设f(x)是定义在区间[a,b]上的一个函数,I是一个确定的数.
若对任给的正数ε,总存在一个正数δ,使得对于区间[a,b]分成n个小区间 [xi-1,xi]的任意分法,只要
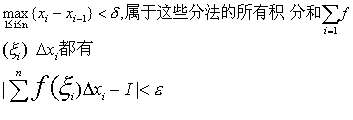 属于这些分法的所有积分和
属于这些分法的所有积分和 (ζi) △xi都有
(ζi) △xi都有![]()
这个定义是法国数学家B.黎曼首先给出的,所以这个意义下的定积分通常称为黎曼积分.
极限
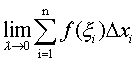 不同于数列极限和函数极限. 当λ→0时,对于λ=max {△xi}的每个值,一般都有无穷多个积分和与它对应,因此,这种极限比数列极限和函数极限复杂. 尽管如此,可积函数的积分和仍保持着与数列极限及函数极限在本质上的相同之处,即当λ→0时,积分和无限接近常数I. 因此,可积函数的积分和有一系列与函数极限类似的性质.
不同于数列极限和函数极限. 当λ→0时,对于λ=max {△xi}的每个值,一般都有无穷多个积分和与它对应,因此,这种极限比数列极限和函数极限复杂. 尽管如此,可积函数的积分和仍保持着与数列极限及函数极限在本质上的相同之处,即当λ→0时,积分和无限接近常数I. 因此,可积函数的积分和有一系列与函数极限类似的性质.定积分的概念来源于几何、物理和其他学科中的一类实际问题. 例如,求某个曲边梯形的面积; 求作变速运动的质点在某一段时间内走过的路程等等. 这类问题的共性是:
❶所求的量都是在某个区间上变化不均匀的整体量;
❷处理这类问题的方法是,先将整体量分为局部量,并求出各局部量的近似值,再求和,以求得整体量的近似值,最后在无限细分的极限过程中求出整体量的精确值. 经过对上述基本思想的概括和抽象,人们建立了定积分的概念.
中学教材中介绍的定积分概念,是定积分的特殊情形. 这种特殊性表现在❶仅就连续函数建立定积分概念. 由于连续函数在闭区间上必可积,因而其和数极限必存在,所以在教材的定义中,直接肯定了和数极限的存在性.
❷在肯定了和数极限存在的前提下,考虑用等分法分割区间 [a,b],于是λ→0便等价于n→∞. 这种特殊的处理方法比较简明易懂,而又不失定积分的基本特征,所以,教材这种安排将有助于学生掌握初等微积分的定积分知识。
☚ 的积分">无理函数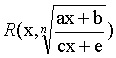 的积分 定积分的几何意义 ☛
的积分 定积分的几何意义 ☛
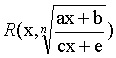 的积分 定积分的几何意义 ☛
的积分 定积分的几何意义 ☛定积分
设函数f(x)是[a,b]上的有界函数,对[a,b]进行任意分割得a0=x0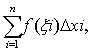 当最大的△xi趋于零且分点无穷多时,上述和式的极限存在,就称此极限值为f(x)在[a,b]上的定积分,记为
当最大的△xi趋于零且分点无穷多时,上述和式的极限存在,就称此极限值为f(x)在[a,b]上的定积分,记为 f(x)dx。如果考虑取函数为二元以上的函数f(x1 ,…,xn)(n=2,3,…,N),类似定积分对自变量的区域进行任意分割,作和,取极限,若极限存在,便称此极限值为f(x1,…,xn)的n重定积分,记为
f(x)dx。如果考虑取函数为二元以上的函数f(x1 ,…,xn)(n=2,3,…,N),类似定积分对自变量的区域进行任意分割,作和,取极限,若极限存在,便称此极限值为f(x1,…,xn)的n重定积分,记为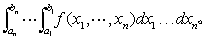 定积分在物理、工程技术等许多领域都有广泛的应用。
定积分在物理、工程技术等许多领域都有广泛的应用。
定积分
definite integral
- r2022090410004808是什么意思
- r2022090410004809是什么意思
- r2022090410004810是什么意思
- r2022090410004811是什么意思
- r2022090410004813是什么意思
- r2022090410004814是什么意思
- r2022090410004815是什么意思
- r2022090410004816是什么意思
- r2022090410004817是什么意思
- r2022090410004818是什么意思
- r2022090410004820是什么意思
- r2022090410004821是什么意思
- r2022090410004823是什么意思
- r2022090410004824是什么意思
- r2022090410004825是什么意思
- r2022090410004826是什么意思
- r2022090410004827是什么意思
- r2022090410004828是什么意思
- r2022090410004830是什么意思
- r2022090410004831是什么意思
- r2022090410004832是什么意思
- r2022090410004833是什么意思
- r2022090410004834是什么意思
- r2022090410004835是什么意思
- r2022090410004837是什么意思
- r2022090410004838是什么意思
- r2022090410004839是什么意思
- r2022090410004840是什么意思
- r2022090410004841是什么意思
- r2022090410004842是什么意思
- r2022090410004843是什么意思
- r2022090410004845是什么意思
- r2022090410004846是什么意思
- r2022090410004848是什么意思
- r2022090410004849是什么意思
- r2022090410004850是什么意思
- r2022090410004851是什么意思
- r2022090410004852是什么意思
- r2022090410004853是什么意思
- r2022090410004854是什么意思
- r2022090410004855是什么意思
- r2022090410004857是什么意思
- r2022090410004858是什么意思
- r2022090410004859是什么意思
- r2022090410004860是什么意思
- r2022090410004861是什么意思
- r2022090410004862是什么意思
- r2022090410004863是什么意思
- r2022090410004864是什么意思
- r2022090410004865是什么意思
- r2022090410004866是什么意思
- r2022090410004867是什么意思
- r2022090410004868是什么意思
- r2022090410004869是什么意思
- r2022090410004870是什么意思
- r2022090410004871是什么意思
- r2022090410004872是什么意思
- r2022090410004873是什么意思
- r2022090410004874是什么意思
- r2022090410004875是什么意思