孙子定理sunzidingli

也叫中国剩余定理，是解一元一次同余式组的方法.我国古代算书《孙子算经》（纪元前后）里提出了下面一个问题：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？答曰二十三.”这个问题实际上就是解一元一次同余式组的问题(参见“一次同余式组”).在《孙子算经》里还提出了许多类似的问题.该书的具体解法可以概括如下：设m₁,m₂，…，m_k是k个两两互质的正整数.令m=m₁m₂…m_k,M_i＝m/m_i,i=1,2，…，k，则同余式组
x≡b₁ (modm₁),x≡b₂ (modm₂)，…，
x≡bk(modm_k).　(1)
对模m有唯一解

x≡M'₁M₁b₁+M'₂M₂b₂+…+M'_kM_kb_k(modm).

其中M'_i满足同余式M'_iM_i≡1 (modm_i),i=1,2，…，k.这个结果通常称为孙子定理.这是在数论中很重要的一个定理.后来这个算法传入西方，被称为中国剩余定理.
现举例说明孙子定理的应用.例如，解一元一次同余式组

x≡1(mod7),x≡3(mod5),x≡5(mod9).

因为7,5,9两两互质，所以可用孙子定理，这时m=7·5·9=315,M₁＝5·9=45,M₂＝7·9=63,M₃＝7·5=35.b₁＝1,b₂＝3,b₃＝5.解同余式M′₁M₁≡1(mod7)，得M′₁＝5，解M′₂M₂≡3 (mod5)，得M′₂＝2，解M′₃M₃≡1 (mod9)，得M′₃＝8.由孙子定理得

x≡5·45·1+2·63·3+8·35·5

≡2 003≡113(mod315).

由此可见，利用孙子定理解同余式组(1)，只要先求出M′_i，则对任意给定的余数bi，都能很容易地求出所需的结果.例如在本条开头所述问题的算法，在我国明代程大位的《算法统宗》(1593)中曾总结成如下的歌诀：

三人同行七十稀，
五树梅花廿一枝，
七子团圆月正半，
除百零五便得知.

意思是说，把用3,5,7除所得余数分别乘以70,21,15再相加，然后从中逐次减去105，即得这个问题的解：x≡2·70+3·21+2·15≡233≡23(mod105).

孙子定理Sunzidingli

两个整数a、b分别除以另一个正整数m，如果余数相同，就称a、b关于模m同余，记作
a≡b (mod m) (1)
这等价于
a=b+mt (t是整数)。
如果a、b是整数， m是正整数， a≠mt (即a0即a0(modm, 我们称
ax≡b(modm) (2)
为关于模m的一次同余式。如果正整数x=c满足(2), 即ac≡b (modm)，那么c称为 (2)的解，而且满足x≡c (modm) 的一切整数都是 (2)的解。对于由n个同余式构成的同余式组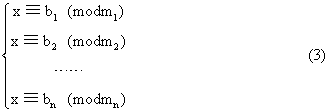
如果正整数x=c同时满足这n个同余式，那么c是这个同余式组的解， 而且满足

x≡c (mod m₁m₂… mn)

的一切整数x都是 (3) 的解。
在中国四、五世纪的《孙子算经》中有一个“物不知数”问题 （参见该条）, 相当于求解同余式组

x≡b₁ (mod3)

x≡b₂ (mod5)
x≡b₃ (mod7)
书中的解说如果推广到一般情形，就是下面的“剩余定理”：
设m₁, m₂, ……，m_n为两两互素的一组正整数，M=m₁m₂…mn, k_i (i=1, 2, …n)是满足下列条件的一组正整数
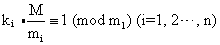
那么 (3) 的最小正整数解是
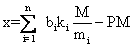
其中p是适当的非负整数。这个定理的一般形式虽然直到13世纪才由中国数学家秦九韶给出，但《孙子算经》中的算法，实际上已经概括了这一定理的结构。在中国古代，从汉代直到宋代，编制历法时都要推算上元积年，所谓上元，是早于制订历法之年的某一时刻，它满足关于太阳、月亮甚至包括金、木、水、火、土五星（近似地）同在一条联线上。而且这一时刻必须是冬至，且发生在夜半 （零时）, 由于日、月、五星的运行周期各不相同，为了求出上元积年，需要求解十分复杂的一次同余式组，而且模数也未必是整数，因而在《孙子算经》的年代，一次同余式组解法及“剩余定理”早已为中国天文学家和数学家所知了，《孙子算经》仅仅是以一个简单的数学模型概括了这一定理。到1247年，南宋数学家秦九韶对各种模数(可以不互素，甚至是小数和分数) 给出了这一问题的完整表述和处理。
19世纪， 秦九韶的工作被西方传教士介绍到欧洲，使欧洲数学家十分惊讶，因为直到19世纪初这一问题在欧洲才由高斯完满地解决， 而中国的有关工作至少早了500多年。因此，上述定理在西方被称为“中国剩余定理”。然而，溯本寻源，在中国最早给出这一定理的数学概括的，是四、五世纪时的《孙子算经》，因此应当称之为 “孙子定理”。