孙子剩余定理

067 孙子剩余定理

由 《孙子算经》 中著名的“物不知数”问题所阐发的关于一次同余式组解法的定理。其一般表达为：设m₁,m₂，…，m_n两两互素，M=m₁m₂…m_n，则同余式组x=b_i(mod m_i) (i=1,2，…，n)有整数解，且对模M唯一。以N表最小正整数解，则

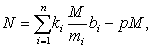
其中k_i满足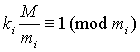(i=1,2，…，n). 整数p可适当选取，使N≤M。《孙子算经》没有给出k_i的求法。南宋秦九韶以“物不知数”问题为基础，系统总结前人成果，于1247年在其所著《数书九章》中提出了求k_i(秦九韶称之为乘率)的程序化方法——大衍求一术。第一次系统完整地给出了一次同余式组的解法。(参见32069大衍求一术)在欧洲，直到18、19世纪，数学家欧拉(L. Euler,1707—1783)、拉格朗日 (J. Lagrange,1736—1813)、高斯 (C. F. Gauss,1777—1855) 等才对一般的一次同余式组进行了详细研究，获得与秦九韶大衍求一术相同的结果。1852年 (英) 伟烈亚力 (A.Wyler,1815—1887)发表《中国科学摘记》，介绍了孙子问题和秦九韶解法，引起西方学者重视。该文先后被译为德文和法文。1876年(德)马蒂森(L.Matthiessen,1830—1906)指出孙子问题的解法与高斯方法完全一致，遂以中国剩余定理命名。现称孙子剩余定理。孙子剩余定理是中国古代数学的辉煌成就之一。它充分体现了中国数学家关于一次同余理论研究的独创性和继承性。在世界数学史上具有崇高的地位。