子对策精练纳什均衡subgame perfect Nash equilibrium

设Γ是有N个局中人的展开型对策。Γ的一个子集G称为Γ的一个子对策，若它满足以下两个条件：
(1)G从某个含惟一决策结点的信息集开始，包含这个结点的所有（直接或间接）后继决策结点，且仅含有这样的结点。
(2)G由若干完整的信息集组成，即若G含信息集H中某点x，则必定包含整个H。
子对策自身组成一个对策，因而可对之应用对策论的结论。
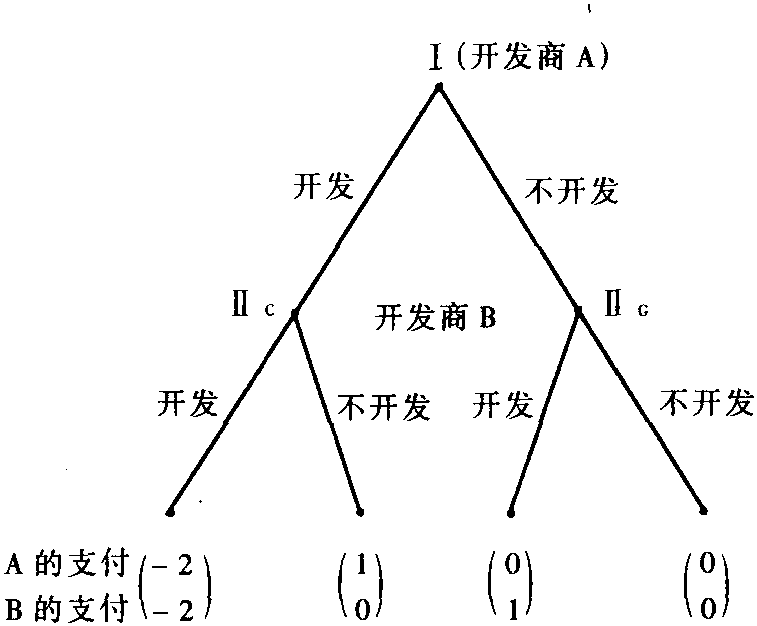
给定Γ的子对策G与Γ的纳什均衡σ。若当G单独考虑时，σ对应G中信息集的那些行为构成G的一个纳什均衡，则说σ在子对策G中导出一个纳什均衡。若σ在Γ的每个子对策中导出一个纳什均衡，则称σ为Γ的子对策精练纳什均衡，简称为SPNE。SPNE必定是纳什均衡，但反之则未必，试看下例。
设Γ是如下图所示的展开型对策。开发商A的策略集S_A＝{开发，不开发}; B的策略集

S_B＝{(开发，开发),(开发，不开发),(不开发，开发),(不开发，不开发)}，其中(开发，开发)表示策略“当A开发时B开发，当A不开发时B开发”，其余类推。Γ可表示如下表所示的标准型对策。这个标准型对策有三个纳什均衡：

(开发，(不开发，开发))、(开发，(不开发，不开发))与(不开发，(开发，开发))。对策Γ有三个子对策：Γ本身及分别从结点Ⅱ_C与Ⅱ_G出发的子对策C与G。因在子对策C内不开发是最优的，而在子对策G内开发是最优的，故(开发，(不开发，开发))分别在C与G内考虑时是纳什均衡，从而它是SPNE。但易于验证，P的其他两个纳什均衡都不是SPNE。