多元直线回归

又称多元线性回归。对两个或多个具自变量与一个因变量之间的线性关系进行回归分析。客观现象之间的联系是复杂的，某一社会现象的变化会受到多种因素的影响。将这一变化的社会现象作为因变量，而将影响因变量变化的各种因素作为各个自变量，如果根据这些自变量与因变量的数值所描述的散点图近似于直线分布，那么就可以建立多元直线回归方程式来分析它们之间的数量关系。多元直线回归方程式一般可表示为：
y_c＝a+b₁x₁+b₂x₂+……+b_kx_k
式中，y_c为因变量y的预测值，a为常数项，x₁x₂……x_k为代表各种因素的自变量，b₁,b₂……b_k为代表各种因素的自变量，b₁,b₂……b_k分别为y对x₁,x₂，……xk的回归系数（又称偏回归系数）,k=1,2,3……。回归系数b₁,b₂，……b_k要通过最小二乘法所建立的如下正规方程组解出：

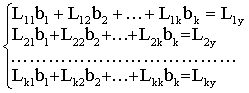
求出b₁,b₂，……b_k值后，常数项a可由下列公式确定：

这时，多元直线回归方程式也就确定了：
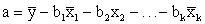
y_c＝a+b₁x₁+b₂x₂+…+b_kx_k利用这一方程式，可以从多种因素的数值变化来预测社会现象的变化趋势。同时，还可通过标准化(即使每一变量值变为标准值，使每一回归系数b变为标准化回归系数B)将原多元直线回归方程变为标准化多元直线回归方程Z_yc＝B₁Z₁+B₂Z₂+…+B_kZ_k，以便有效地比较各个自变量影响因变量Y的作用大小