多个样本均数间两两比较

多个样本均数作比较时，经方差分析，若认为各总体均数间有差别，常需进一步确定哪两个总体均数间有差别，哪两个间没有差别。为此，可利用方差分析提供的信息作样本均数间的两两比较，又称多重比较。如A、B、C三个样本均数的两两比较有A与B、B与C、A与C三种情况；A、B、C、D四个样本均数的两两比较有六种情况；k个样本均数比较有(k₂)=k(k-1)/2种情况。进行两两比较有多种方法，本条目介绍Newman-Keuls检验、Duncan检验、Tukey检验、最小显著差检验及Scheffe检验。它们的理论依据、应用条件有所不同，其中前二种较为多用。
Newman-Keuls检验 (D.Newman,1939; M.Ke-uls,1952) 亦称Student-Newman-Kenls (SNK)检验。计算统计量q值的公式为

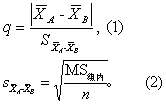
式中A-B为两两比较中的任何两个对比组均数之差值；为差值的标准误；MS组内为方差分析的组内均方； n为各样本的例数或平均例数。本法步骤如下：
(1)将k组的均数从大到小排列：，然后按其顺序列出对比组，如表6第(1)栏为对比组的代号，即从最大均数开始，顺次与其他各组对比；然后以次大均数与各组对比，依此类推。
(2) 计算对比组的两均数之差，如表6第(2)栏。
(3) 写出均数按大小排列时，两对比组范围内包含的组数α。 如与对比，α=2;与对比，α=3;与对比，α=k，如表6第(3)栏。
(4)将方差分析表中MS组内代入式(2)得sA-B，将其与两均数之差代入式(1)得q值。如表6第(4)栏。
(5) 按MS组内的自由度v和组数α查表1q界值表得P值，按所取检验水准作出推断结论。
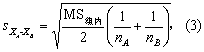
若各组例数不等，只须将式(2)改为式(3)即可，其余步骤不变。

式中nA与nB分别为第A组与第B组的例数。
Duncan检验(D.B.Duncan,1955) 亦称Duncan新法，以区别于Duncan于1951年提出的方法。本法除用表2q界值表代替表1外，其余同Newman-Keuls检验，包括各组例数不同的处理。表2与表1不同的是当α≥3时表2的q界值皆小于表1的相应界值。
Tukey检验(J.W.Tukey,1953) 本法要求各组例数相等。它与Newman-Keuls检验不同的只是不论α值大小，一律用组数α=k（即比较的全部组数）查表1q界值表。因此对同一资料，Tukey检验的界值即New-man-Keuls检验的最大界值。
最小显著差(LSD)检验 本法要求各组例数相等。它与Newman-Keuls检验不同的只是不论α值大小，一律用组数α=2查表1q界值表。因此对同一资料本法界值即Newman-Keuls检验的最小界值。

表1 Newman-Keuls检验用q界值表
上行：P=0.05，下行：P=0.01

v	组 数，a
	2	3	4	5	6	7	8	9	10
5	3.64 5.70	4.60 6.98	5.22 7.80	5.67 8.42	6.03 8.91	6.33 9.32	6.58 9.67	6.80 9.97	6.99 10.24
6	3.46 5.24	4.34 6.33	4.90 7.03	5.30 7.56	5.63 7.97	5.90 8.32	6.12 8.61	6.32 8.87	6.49 9.10
7	3.34 4.95	4.16 5.92	4.68 6.54	5.06 7.01	5.36 7.37	5.61 7.68	5.82 7.94	6.00 8.17	6.16 8.37
8	3.26 4.75	4.04 5.64	4.53 6.20	4.89 6.62	5.17 6.96	5.40 7.24	5.60 7.47	5.77 7.68	5.92 7.86
9	3.20 4.60	3.95 5.43	4.41 5.96	4.76 6.35	5.02 6.66	5.24 6.91	5.43 7.13	5.59 7.33	5.74 7.49
10	3.15 4.48	3.88 5.27	4.33 5.77	4.65 6.14	4.91 6.43	5.12 6.67	5.30 6.87	5.46 7.05	5.60 7.21
12	3.08 4.32	3.77 5.05	4.20 5.50	4.51 5.84	4.75 6.10	4.95 6.32	5.12 6.51	5.27 6.67	5.39 6.81
14	3.03 4.21	3.70 4.89	4.11 5.32	4.41 5.63	4.64 5.88	4.83 6.08	4.99 6.26	5.13 6.41	5.25 6.54
16	3.00 4.13	3.65 4.79	4.05 5.19	4.33 5.49	4.56 5.72	4.74 5.92	4.90 6.08	5.03 6.22	5.15 6.35
18	2.97 4.07	3.61 4.70	4.00 5.09	4.28 5.38	4.49 5.60	4.67 5.79	4.82 5.94	4.96 6.08	5.07 6.20
20	2.95 4.02	3.58 4.64	3.96 5.02	4.23 5.29	4.45 5.51	4.62 5.69	4.77 5.84	4.90 5.97	5.01 6.09
30	2.89 3.89	3.49 4.45	3.85 4.80	4.10 5.05	4.30 5.24	4.46 5.40	4.60 5.54	4.72 5.65	4.82 5.76
40	2.86 3.82	3.44 4.37	3.79 4.70	4.04 4.93	4.23 5.11	4.39 5.26	4.52 5.39	4.63 5.50	4.73 5.60
60	2.83 3.76	3.40 4.28	3.74 4.59	3.98 4.82	4.16 4.99	4.31 5.13	4.44 5.25	4.55 5.36	4.65 5.45
120	2.80 3.70	3.36 4.20	3.68 4.50	3.92 4.71	4.10 4.87	4.24 5.01	4.36 5.12	4.47 5.21	4.56 5.30
∞	2.77 3.64	3.31 4.12	3.63 4.40	3.86 4.60	4.03 4.76	4.17 4.88	4.29 4.99	4.39 5.08	4.47 5.16

摘自 Beyer WH:Handbook of Tables for Probabi lity and Statistics,second edition,p362,p364，CRC Press,Inc.,1979

表2 Duncan检验用q界值表
上行： P=0.05，下行： P=0.01

v	组 数，a
	2	3	4	5	6	7	8	9	10
5	3.64 5.70	3.74 5.96	3.79 6.11	3.83 6.18	3.83 6.26	3.83 6.33	3.83 6.40	3.83 6.44	3.83 6.5
6	3.46 5.24	3.58 5.51	3.64 5.65	3.68 5.73	3.68 5.81	3.68 5.88	3.68 5.95	3.68 6.00	3.68 6.0
7	3.35 4.95	3.47 5.22	3.54 5.37	3.58 5.45	3.60 5.53	3.61 5.61	3.61 5.69	3.61 5.73	3.61 5.8
8	3.26 4.74	3.39 5.00	3.47 5.14	3.52 5.23	3.55 5.32	3.56 5.40	3.56 5.47	3.56 5.51	3.56 5.5
9	3.20 4.60	3.34 4.86	3.41 4.99	3.47 5.08	3.50 5.17	3.52 5.25	3.52 5.32	3.52 5.36	3.52 5.4
10	3.15 4.48	3.30 4.73	3.37 4.88	3.43 4.96	3.46 5.06	3.47 5.13	3.47 5.20	3.47 5.24	3.47 5.28
12	3.08 4.32	3.23 4.55	3.33 4.68	3.36 4.76	3.40 4.84	3.42 4.92	3.44 4.96	3.44 5.02	3.46 5.07
14	3.03 4.21	3.18 4.42	3.27 4.55	3.33 4.63	3.37 4.70	3.39 4.78	3.41 4.83	3.42 4.87	3.44 4.91
16	3.00 4.13	3.15 4.34	3.23 4.45	3.30 4.54	3.34 4.60	3.37 4.67	3.39 4.72	3.41 4.76	3.43 4.79
18	2.97 4.07	3.12 4.27	3.21 4.38	3.27 4.46	3.32 4.53	3.35 4.59	3.37 4.64	3.39 4.68	3.41 4.71
20	2.95 4.02	3.10 4.22	3.18 4.33	3.25 4.40	3.30 4.47	3.34 4.53	3.36 4.58	3.38 4.61	3.40 4.65
30	2.89 3.89	3.04 4.06	3.12 4.16	3.20 4.22	3.25 4.32	3.29 4.36	3.32 4.41	3.35 4.45	3.37 4.48
40	2.86 3.82	3.01 3.99	3.10 4.10	3.17 4.17	3.22 4.24	3.27 4.30	3.30 4.34	3.33 4.37	3.35 4.41
60	2.83 3.76	2.98 3.92	3.08 4.03	3.14 4.12	3.20 4.17	3.24 4.23	3.28 4.27	3.31 4.31	3.33 4.34
100	2.80 3.71	2.95 3.86	3.05 3.98	3.12 4.06	3.18 4.11	3.22 4.17	3.26 4.21	3.29 4.25	3.32 4.29
∞	2.77 3.64	2.92 3.80	3.02 3.90	3.09 3.98	3.15 4.04	3.19 4.09	3.23 4.14	3.26 4.17	3.29 4.20

摘自 Duncan DB: Multiple range and multiple F tests,Biometrics,11: 1,1955
Scheffe检验(H. Schffe,1959) 用式(4)、式(5)计算统计量S值。

注意：式(4)与式(1)相似，但式(5)与式(3)不同。经F检验多个样本均数间有差别，则用Scheffe检验一定可找到有差别的对比组。求得S值后，查表3 S界值表得P值，按所取检验水准作出推断结论。表3中的v亦为MS组内的自由度，k为处理组的个数。由此可见，此表与a无关。

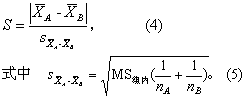
表3 Scheffé检验用S界值表
上行： P=0.05，下行 P=0.01

v	k-1
	2	3	4	5	6	7	8	9	10
5	3.40 5.15	4.03 6.01	4.56 6.75	5.03 7.41	5.45 8.00	5.84 8.56	6.21 9.07	6.55 9.56	6.88 10.03
6	3.21 4.67	3.78 5.42	4.26 6.05	4.68 6.61	5.07 7.13	5.43 7.60	5.76 8.05	6.07 8.47	6.37 8.87
7	3.08 4.37	3.61 5.04	4.06 5.60	4.46 6.11	4.82 6.57	5.15 7.00	5.46 7.40	5.75 7.78	6.03 8.14
8	2.99 4.16	3.49 4.77	3.92 5.29	4.29 5.76	4.64 6.18	4.95 6.58	5.24 6.94	5.52 7.29	5.79 7.63
9	2.92 4.01	3.40 4.58	3.81 5.07	4.17 5.50	4.50 5.90	4.80 6.27	5.08 6.61	5.35 6.94	5.60 7.25
10	2.86 3.89	3.34 4.43	3.73 4.90	4.08 5.31	4.39 5.68	4.68 6.03	4.96 6.36	5.21 6.67	5.46 6.96
12	2.79 3.72	3.24 4.23	3.61 4.65	3.94 5.03	4.24 5.38	4.52 5.70	4.77 6.00	5.02 6.28	5.25 6.55
14	2.73 3.61	3.17 4.09	3.53 4.49	3.85 4.85	4.13 5.17	4.40 5.47	4.65 5.75	4.88 6.02	5.10 6.28
16	2.70 3.53	3.12 3.98	3.47 4.37	3.78 4.71	4.06 5.02	4.31 5.31	4.55 5.58	4.78 5.83	4.99 6.08
18	2.67 3.47	3.08 3.91	3.42 4.28	3.72 4.61	4.00 4.91	4.25 5.19	4.48 5.44	4.70 5.69	4.91 5.92
20	2.64 3.42	3.05 3.85	3.39 4.21	3.68 4.53	3.95 4.82	4.20 5.09	4.42 5.34	4.64 5.58	4.85 5.80
30	2.58 3.28	2.96 3.68	3.28 4.01	3.56 4.30	3.81 4.57	4.04 4.81	4.26 5.04	4.46 5.25	4.65 5.46
40	2.54 3.22	2.92 3.60	3.23 3.91	3.50 4.19	3.74 4.44	3.97 4.68	4.18 4.89	4.37 5.10	4.56 5.29
60	2.51 3.16	2.88 3.52	3.18 3.82	3.44 4.09	3.68 4.33	3.89 4.55	4.10 4.75	4.28 4.95	4.46 5.13
120	2.48 3.09	2.84 3.44	3.13 3.73	3.38 3.98	3.61 4.21	3.82 4.42	4.02 4.62	4.20 4.80	4.37 4.97
∞	2.45 3.03	2.80 3.37	3.08 3.64	3.33 3.88	3.55 4.10	3.75 4.30	3.94 4.48	4.11 4.65	4.28 4.82

摘自 山内二郎：統計数值表，66,JSA-1972。
例1 用四种饲料喂大白鼠，测得其肝重占体重的百分比值见表4，经方差分析见表5，得P<0.01，故认为不同饲料组的肝重比值有差别。为获得进一步的结论，试进行两两比较。

表4 四种饲料喂大白鼠后的肝重比值(%)

	I号	II号	III号	IV号
X	2.62 2.23 2.36 2.40	2.82 2.76 2.43 2.73	2.91 3.02 3.28 3.18	3.92 3.02 3.30 3.04
	2.40	2.69	3.10	3.32

表5 表3资料的方差分析

变异来源	SS	v	MS	F
总	2.807375	15
组 间 组 内	2.027525 0.779850	3 12	0.6758 0.0650	10.40

H₀: μA=μB，即各总体均数两两相等；
H₁: μA≠μB，即各总体均数不等或不全相等。
α=0.05。
(1) Newman-Keuls检验。
四组均数按大小顺序排列

IV号	III号	II号	I号
3.32	3.10	2.69	2.40

各对比组、两均数之差、组数α见表6第(1)～(3)栏。按式(2)得

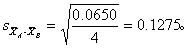
按式(1)得各对比组q值，见表6第(4)栏。
以v=12及α查表1得各P值，见表6第(5)栏。

表6 四种饲料组肝重比值均数间的两两比较

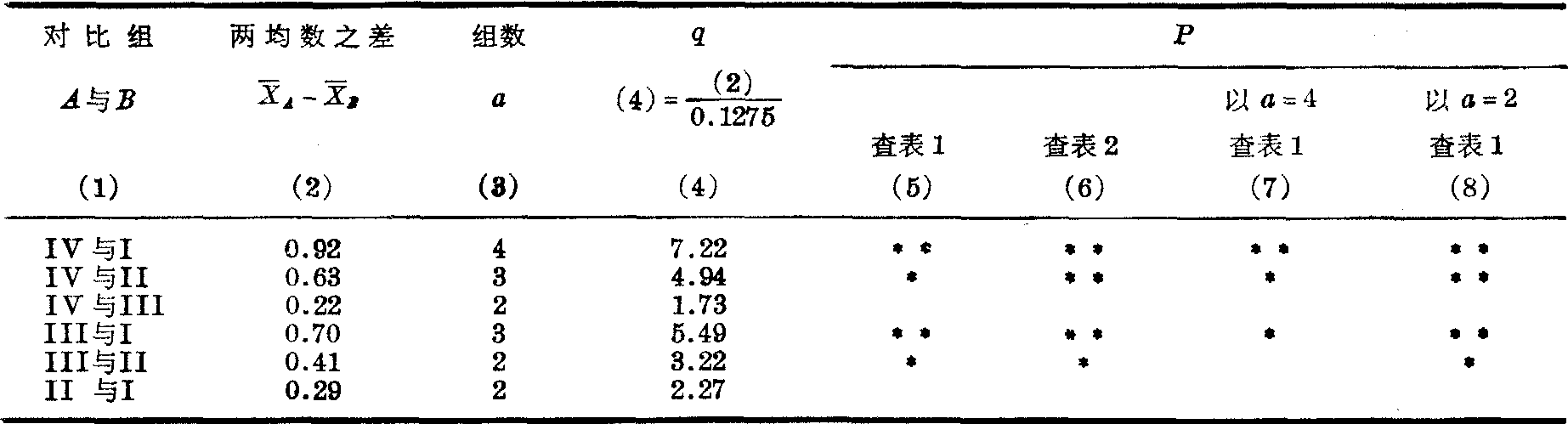
*表示P<0.05,**表示P<0.01，无*表示P>0.05。
(2) Duncan检验。得表6第(1)～(4)栏后，以v=12及α查表2得各P值，见表6第(6)栏。
(3) Tukey检验。得表6第(1)、(2)、(4)栏后，以v=12,α=4查表1得各P值，见表6第(7)栏。
(4)最小显著差检验。得表6第(1)、(2)、(4)栏后，以v=12,α=2查表1得各P值，见表6第(8)栏。
由表6第(5)～(8)栏可见：按α=0.05水准，四种方法检验结论基本一致：除Ⅰ、Ⅱ号饲料间及Ⅲ、Ⅳ号饲料间肝重比值无差别(均不拒绝H0)外，其余的任何两种饲料间肝重比值均有差别(Ⅲ与Ⅱ比较除Tukey检验为P>0.05外，其他三法都是P<0.05，均拒绝H₀，接受H₁)，可以认为喂Ⅲ、Ⅳ号饲料大白鼠的肝重比值较喂Ⅰ、Ⅱ号的为高。
例2 三种药分别用于小白鼠后，平均延迟咳嗽时间见表7，经方差分析(表8)，得P<0.05，可认为三种药的延迟咳嗽时间不同。为获得进一步的结论，试进行两两比较。

表7 三种药使小白鼠平均延迟咳嗽时间

药 物	例 数 n	平均延迟时间（秒） 
复方一(I) 复方二(II) 可待因(III)	15 15 10	31.67 44.00 60.50

表8 方差分析

变异来源	SS	v	MS	F
总	31810.00	39
组 间 组 内	4994.17 26815.83	2 37	2497.08 724.75	3.45

H_0:μ A=μB,
H₁: μA≠μB。
α=0.05。
(1) Newman-Keuls检验。按式(3)得

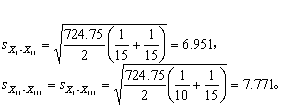
得表9第(1)～(4)栏后，以v=37及α查表1得各P值，P<0.05者在q值右上角记“*”，P>0.05者无“*”。
(2) Duncan检验。得表9第(1)～(4)栏后，以v=37及α查表2得各P值，结果同Newman-Keuls检验。
(3) Scheffe检验。按式(5)

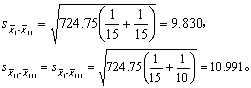
得表9第(1)、(2)栏及第(5)栏[按式(4)]后，以v=37,k=3查表3得各P值，P<0.05者在S值右上角记“*”，P>0.05者无“*”。
表9 三种药平均延迟咳嗽时间的两两比较
上述三种方法检验结果按a = 0.05水准结论相同，即可以认为三种药中可待因延迟小白鼠咳嗽的时间比复方一长，其余没有差别。
多组均数间的两两比较时应注意：
(1) 如果都用t检验来推断，则将明显增大Ⅰ型错误a。例如作t检验时的a=0.05，共需作6个比较，则6次t检验的实际水准变为1-(1-0.05)＝0.265, 比0.05大多了。
(2) Newman-Keuls检验和Duncan检验由于采用多重界值，故检验的准确性较高。四种方法的敏感度不同： 最小显著差检验最大 (由于一律用a=2时的界值，界点最低),Duncan检验次之，Newman-Keuls检验又次之 (此法除a=2外，界值均较Duncan检验为高),Tukey检验最低 (由于一律用a=k时的界值，界点最高)。