多个方差的齐性检验

已知多个样本（理论上均来自正态总体）方差，可据此推断它们分别代表的总体方差是否相等，即多个方差的齐性检验(参见条目“两个方差的齐性检验)。常用于：
❶说明多组变量值的变异度有无差别。
❷为了比较多个样本均数而作方差分析时，须进行方差齐性检验。如方差齐，宜用F检验；方差不齐宜用F'检验或其他方法。多个方差的齐性检验最常用的是Bartlett检验 (M. S.Bartlett,1937)。
Bartlett检验时须计算统计量x²_C值，根据各样本含量是否相等，x²_C值的算法略有不同：
(1) 当各样本含量相等时，用式(1)或式(2)计算x²值，再用式(S)求其校正值x²_C。

式(1)用自然对数，式(2)用常用对数，二者结果相同，式(3)是为了校正。式中n为每个样本的含量；k为样本个数；sⁱ₂为各样本的方差；s²_C为合并方差，当各样本含量相同时，s²_C＝∑s²_i/k;v为自由度。
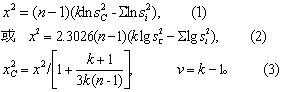
(2) 当各样本含量不等时，须先用式(4)计算合并方差s²_C

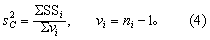
式中SS_i为各样本的离均差平方和，v_i为各样本的自由度，n_i为各样本含量。
再用式(5)或式(6)计算x²值，最后用式(7)求其校正值x²C。

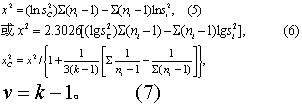
式中n_i为各样木含量，其余符号同前。
求得x²_C值后，查x²界值表得P值，按所取检验水准作出推断结论。
例1 试检验表1八个方差的齐性。

表1 八个样本的观察值X及其方差

	样 本
	1	2	3	4	5	6	7	8
X	91.9 86.9 103.0 102.3	71.5 73.6 81.3 52.8	53.0 55.5 57.3 105.5	96.2 74.4 117.6 103.3	105.9 87.9 82.0 120.5	69.4 60.8 82.3 37.0	99.8 87.9 59.4 61.8	99.3 106.4 82.2 118.0
g2	61.54	146.19	633.96	324.13	307.35	364.24	393.08	224.53

H₀:八个总体方差相等，
H₁:八个总体方差不等或不全相等。
α=0.05。
按式(1)及式(3):

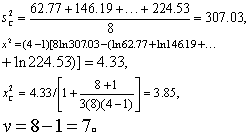
查x²界值表得0.95>P>0.50，按α=0.05水准不拒绝H0，故可认为八个总体方差齐。
例2 丙烯腈和乙腈毒性联合作用实验，取家兔22只，用四种不同浓度染毒2月后测定血中硫氰酸盐含量(mg/L)，结果见表2，检验四组方差的齐性。

表2 四组测定值的方差齐性检验

	对照组	低浓度	中浓度	高浓度
X	2.1 3.1 2.0 1.4	7.3 4.6 3.0 10.5 7.6 14.3 7.8	35.0 50.0 25.0 29.0 60.0	90.0 90.5 91.0 78.0 70.5 79.6
∑X ni i SSi s2i	8.6 4 2.15 1.49 0.4967	55.1 7 7.87 83.07 13.8457	199 5 39.8 870.80 217.7000	499.6 6 83.27 361.63 72.3267

H₀:四个总体方差相等，
H₁:四个总体方差不等或不全相等。
a=0.05。
按式(4)、式(5)、式(7):

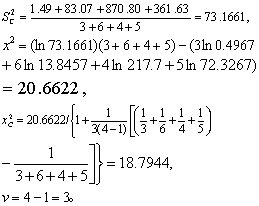
查x²界值表得P<0.005，按a=0.05水准拒绝H0，接受H₁，故可认为四组的方差不齐。