复数的减法
复数的减法fushu de jianfa
加法的逆运算,即把满足
(c+di)+(x+yi)=a+bi
的复数x+yi叫做复数a+bi减去复数c+di所得的差.记作(a+bi)-(c+di).由复数相等的意义易得出x=a-c,y=b-d.于是有(a+bi)-(c+di)=(a-c)+(b-d)i
因为-c-di是c+di的相反复数,而(a+bi)+(-c-di)=(a-c)+(b-d)i=(a+bi)-(c+di).所以复数减法法则是:减去某复数等于加上它的相反复数.显然两个复数的差仍是一个复数.若复数z=a+bi对应的向量是
 ,z1=c+di对应的向量是
,z1=c+di对应的向量是 容易证明复数z=a+bi减去复数z1=c+di所得的差z2=(a-c)+(b-d)i所对应的向量就是
容易证明复数z=a+bi减去复数z1=c+di所得的差z2=(a-c)+(b-d)i所对应的向量就是 (如图),即连结两个向量终点并指向被减数的向量.这也是复数减法的几何解释(几何意义)及用求向量差的三角形法则来进行两个复数相减的几何方法.
(如图),即连结两个向量终点并指向被减数的向量.这也是复数减法的几何解释(几何意义)及用求向量差的三角形法则来进行两个复数相减的几何方法.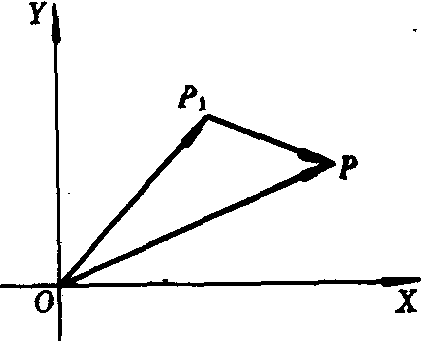
☚ 复数的相反数 复数减法法则 ☛
- 令节拜天是什么意思
- 令节设供是什么意思
- 令芳是什么意思
- 令苛不听是什么意思
- 令苛则不听,禁多则不行是什么意思
- 令范是什么意思
- 令荆是什么意思
- 令草是什么意思
- 令行头是什么意思
- 令行如流是什么意思
- 令行无变,兵行无猜是什么意思
- 令行无变,兵行无猜,轻者若霆,奋敌若惊。是什么意思
- 令行禁止是什么意思
- 令行禁止,为国之关楗。是什么意思
- 令行禁止,王之始也是什么意思
- 令行禁止,王者之师也。是什么意思
- 令行禁止;言出法随是什么意思
- 令言是什么意思
- 令誉是什么意思
- 令誉许文休是什么意思
- 令诒是什么意思
- 令谟是什么意思
- 令贡举人勉学诏是什么意思
- 令贤妹是什么意思
- 令质是什么意思
- 令贵人往实广虚之地是什么意思
- 令贻是什么意思
- 令蹤是什么意思
- 令辞是什么意思
- 令辟是什么意思
- 令辰是什么意思
- 令远是什么意思
- 令通是什么意思
- 令邑是什么意思
- 令邦是什么意思
- 令郎是什么意思
- 令郎君是什么意思
- 令郎捷对 高明是什么意思
- 令酒是什么意思
- 令重是什么意思
- 令重于宝,不为重宝轻号令是什么意思
- 令重于宝,社稷先于亲戚。是什么意思
- 令钦是什么意思
- 令钩是什么意思
- 令长是什么意思
- 令长丞尉是什么意思
- 令长新戒是什么意思
- 令问是什么意思
- 令闻是什么意思
- 令闻令望是什么意思
- 令闻嘉誉是什么意思
- 令闻广誉是什么意思
- 令闻美誉是什么意思
- 令阁是什么意思
- 令阃是什么意思
- 令阮是什么意思
- 令雒州举人诏是什么意思
- 令雨是什么意思
- 令面光华方是什么意思
- 令顺民心则威令行;使民各为其所长则用备。是什么意思