圆系
圆系yuanxi
具有某一共同性质的圆的集合.它们的方程叫做圆系方程.
在圆的方程(x-a)2+(y-b)2=r2或x2+y2+Dx+Ey+F=0中,固定两个(或一个)系数,而另一个(或两个)系数可在实数集内取其允许值,则方程就成为圆系方程.含有可变的系数(称为参数)是圆系方程的基本特征.
常见的圆系有:
❶同心圆系.在方程(x-a)2+(y-b)2=r2中,固定a和b的值,使r取不同的正实数值,构成一个同心圆系.
❷共轴圆系.共根轴的圆系叫做共轴圆系,共轴圆系的方程是x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0,其中λ为不等于-1的任意实数,此圆系中不包括第二个圆,λ=-1时,方程(D1-D2)x+(E1-E2) y+(F1-F2)=0表示根轴.共轴圆系方程可简化写作C1+λC2=0.当圆C1和圆C2相交时,方程表示过两圆交点的圆系,根轴就是公共弦所在直线(如图1);当圆C1和圆C2相切(内切或外切)时,方程表示过两圆的切点且和它们都相切于该点的圆系,根轴就是公切线(如图2);当圆C1和圆C2没有公共点(外离或内含)时,圆系中任何两圆都没有公共点,根轴也和圆系中任何一圆没有公共点(如图3).
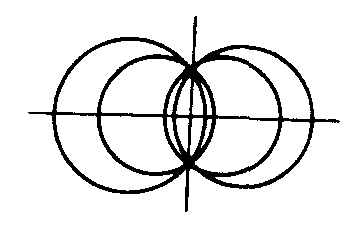
图1
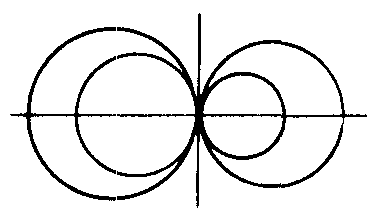
图2
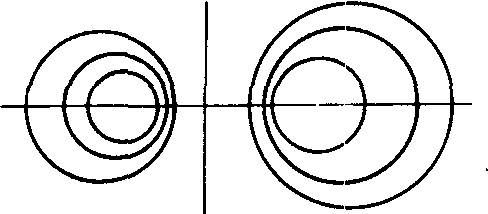
图3
求过已知两圆交点的圆的方程时,可以先设为C1+λC2=0,然后用待定系数法求出λ的值,便可得到所求圆的方程.
☚ 三个圆的根心 椭圆 ☛
圆系
system of circles
- 上气丸是什么意思
- 上气候导引法是什么意思
- 上水是什么意思
- 上水是什么意思
- 上水船是什么意思
- 上水船是什么意思
- 上水船是什么意思
- 上水船是什么意思
- 上水鱼疔是什么意思
- 上求下告是什么意思
- 上江是什么意思
- 上江是什么意思
- 上池杂著 明 冯时可是什么意思
- 上池杂说是什么意思
- 上池杂说是什么意思
- 上池水是什么意思
- 上池水(饮上池)是什么意思
- 上池涓滴是什么意思
- 上池涓滴是什么意思
- 上池饮是什么意思
- 上池饮是什么意思
- 上油是什么意思
- 上法是什么意思
- 上法不上贤是什么意思
- 上洛是什么意思
- 上洞小丹是什么意思
- 上流是什么意思
- 上流是什么意思
- 上流头是什么意思
- 上流社会是什么意思
- 上测是什么意思
- 上浮是什么意思
- 上海是什么意思
- 上海是什么意思
- 上海是什么意思
- 上海是什么意思
- 上海是什么意思
- 上海是什么意思
- 上海700年是什么意思
- 上海——冒险家的乐园是什么意思
- 上海——现代中国的钥匙是什么意思
- 上海—易初摩托车有限公司是什么意思
- 上海“孤岛”文学回忆录是什么意思
- 上海“孤岛”文学报刊编目是什么意思
- 上海“孤岛”时期重振杂文和散文的呼声是什么意思
- 上海《泰晤士报》评论“宝城铁路之重要性”是什么意思
- 上海一日是什么意思
- 上海一日是什么意思
- 上海一日是什么意思
- 上海一日的征文运动是什么意思
- 上海万国证券股份有限公司是什么意思
- 上海不锈钢厨房设备厂是什么意思
- 上海不锈钢器皿厂是什么意思
- 上海世界语协会是什么意思
- 上海业余剧人协会是什么意思
- 上海业余剧人协会是什么意思
- 上海业余剧人协会是什么意思
- 上海业余剧人协会是什么意思
- 上海业余戏剧交谊社是什么意思
- 上海业余戏剧交谊社是什么意思