圆形分布法

圆形分布法用于角度、昼夜时间等资料的分析，通过三角函数变换，使原始数据成为线性资料。本条目主要介绍角度数据的图示、均数及标准差，并用参数及非参数法作假设检验，进行样本间的比较。
医学上有些资料是用角度表示的，如心电向量图的电轴、脑血流图的主峰角；或用昼夜时间表示的，如疾病发作时间。这类数据的特点是具有“周期性”，往往形成“圆形分布”。在圆形分布上，不但没有真正的零点，而且数值大小的意义也是特定的。一个圆分为360°(或2π弧度)，按罗盘标记东南西北，〔见图1(a)〕，但无法证明正北方向就是0°(或360°)，也不能说90°的方向“大于”60°的。设有三个角度值——10°、30°、350°，如果用通常方法求均数： (10°+30°+350°)/3=130°，显然不合理，因为三个角本来都指向偏北方，而“平均角”却指向东南方。又如一昼夜24小时，可用圆形表示，如图1(b),1点、2点、23点都在夜里，而“平均时”为8点40分，却在上午，也不合理。其他时间划分如月份也可用圆形分布表示。

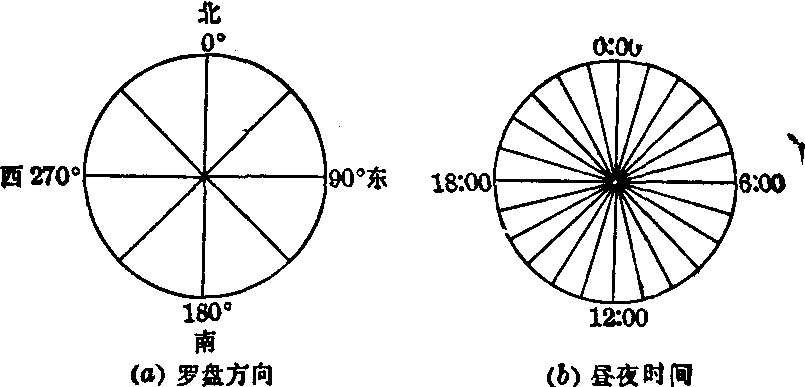
图1 常用圆形标度

应用圆形分布法的条件是：
❶资料呈单峰分布；
❷角度资料要准确到度，昼夜时间要准确到几点几分；
❸圆形分布的角度表示法与三角学有区别，但仍须查三角函数表；
❹资料的具体单位要换算为角度，如1小时相当于15°,1分钟相当于0.25°或15’。余类推。
圆形分布资料常用散布图表示。例数较少时，可将变量值直接在圆周上作点，以示分布，如例1；例数较多时，以同心圆表示例数（或占总例数的构成比）的尺度，以相应位置上的半径长度表示频数分布，如例2。
例1 图示11名11～12岁儿童的心电向量图额面QRS心电轴的角（度）:
-22,6,38,44,48,58,70,77,79,82,86
将这些数据在圆周上作点，见图2。例2 用表1资料绘制频数分布图。
角度自0°开始，顺时针方向为正，逆时针方向为负，在组中值位置上以各组段频数为半径作图，见图3。

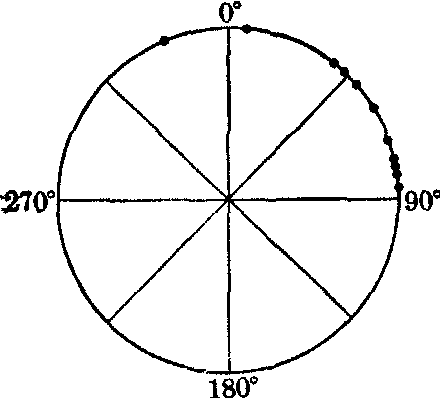
图2 11名儿童QRS心
电轴角度分布

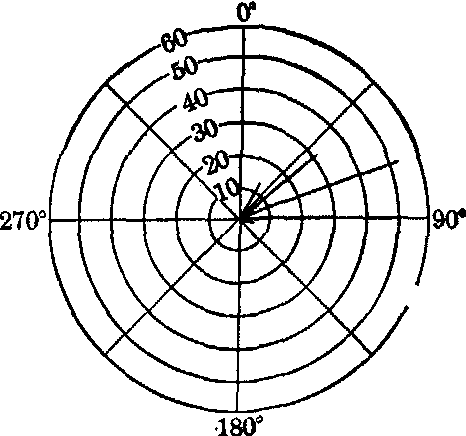
图3 7～9岁儿童129人
心电轴资料图示

表1 7～9岁儿童129人的心电轴（度）

组 段	组中值	频 数
-90～ -20～ 0～ 20～ 40～ 60～ 80～	-55 -10 10 30 50 70 90	1 1 2 13 31 53 24
100～120	110	4
		129

角均数 亦称平均角。令ai表示a₁, a₂，…an角，ā表示样本角均数，它是总体角均数μa的估计值。求ā的公式为

式中r表示集中的度量（不是样本相关系数），没有单位。r的数值自0～1:若r=0，表示没有一个平均的方向，即角的均数是不明确的；若r=1，表示全部数据都集中在同一方向。 注意：从sinā与cosā所得ā应相等，否则计算有错误。有时查出的两个角互为补角，尤其在正弦或余弦值为负时，注意该角所在的象限。
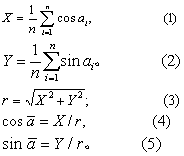
例3 计算表1资料的角均数。

表2 角均数的计算

心电轴（度）,a (1)	频数，f (2)	fsina (3)	fcosa (4)
-55 -10 10 30 50 70 90 110	1 1 2 13 31 53 24 4	-0.819152 -0.173648 0.347296 6.500000 23.747378 49.803709 24.000000 3.758770	0.573576 0.984808 1.969616 11.258330 19.926416 18.127068 0 -1.368081
合 计	129	107.164353 (∑sina)	51.471733 (∑cosa)

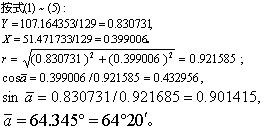
角标准差 亦称圆形标准差或平均角离差，简称角离差，符号为s，是表示圆形分布变异程度的指标，计算公式为

理论上s值的范围自0至∞，与通常的标准差类似。若将自然对数化成常用对数，则式(6)、(7)变成式 (8)、(9)。

式(9)对于生物学及医学都很有用。r与s是样本统计量，相应的总体参数为ρ与σ。角的数值愈集中，r值愈大，s值愈小；角的数值愈分散，r值愈小，s值愈大。
例4 求下列六个样本的角均数ā与r、标准差s。

样本号	原 始 数 据 （度）,a
1 2 3 4 5 6	50 40 10 -45 -75 -105	50 42 30 10 -15 -45	50 48 45 40 35 15	50 52 55 60 65 75	50 58 70 90 109.15 135	50 60 90 135 170 195

以5号样本为例，按式(1)～(5)及式(9)说明计算过程：
角中有6个小于它，5个大于它。二项分布的均数nπ=11/2=5.5。在62°两边角的个数X各为6和5，它们与均数距离的绝对值均为0.5。当X为7及以上或4及以下时，X与均数距离的绝对值都大于0.5，出现这些X值的概率由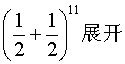式求得为

P=0.274414×2=0.548828，即P>0.05，故不拒绝总体中位角为62°的检验假设。
两样本角均数的比较 亦称Watson-Williams检验(G.S.Watson与E.J.Williams)，按式(11)计算统计量F值，作F检验。

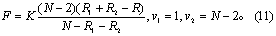
式中N为两样本含量n₁及n₂之和；R₁与R2由两样本分别按式(10)算得；R为两样本合并后求出的R值；K为计算F值的校正因子，由r值查表4即得。当r=R/N在0.70以上时式(11)较适用。求得F值后，查F界值表得P值，按所取检验水准作出推断结论。当v1=1时，＝t，而t值的自由度同v₂＝N-2，查t界值表，得P值相同。
多个样本角均数的比较 上述Watson-Williams检验法可推广到多个样本角均数的比较，须按式(12)计算

表4 Watson-Williams检验用校正因子K

r	K	r	K	r	K	r	K
.00		.25 .26 .27 .28 .29	1.7261 1.6962 1.6685 1.6427 1.6186	.50 .51 .52 .53 .54	1.3235 1.3148 1.3065 1.2984 1.2905	.75 .76 .77 .78 .79	1.1583 1.1528 1.1472 1.1417 1.1362
.01 .02 .03 .04	19.7500 10.3727 7.2469 5.6840
.05 .06 .07 .08 .09	4.7451 4.1193 3.6721 3.3363 3.0749	.30 .31 .32 .33 .34	1.5960 1.5748 1.5548 1.5360 1.5183	.55 .56 .57 .58 .59	1.2829 1.2754 1.2682 1.2611 1.2542	.80 .81 .82 .83 .84	1.1306 1.1250 1.1193 1.1136 1.1078
.10 .11 .12 .13 .14	2.8656 2.6942 2.5512 2.4300 2.3261	.35 .36 .37 .38 .39	1.5015 1.4855 1.4703 1.4559 1.4422	.60 .61 .62 .63 .64	1.2474 1.2408 1.2343 1.2280 1.2217	.85 .86 .87 .88 .89	1.1019 1.0959 1.0898 1.0835 1.0772
.15 .16 .17 .18 .19	2.2358 2.1567 2.0869 2.0246 1.9688	.40 .41 .42 .43 .44	1.4290 1.4165 1.4044 1.3929 1.3818	.65 .66 .67 .68 .69	1.2156 1.2096 1.2036 1.1077 1.1920	.90 .91 .92 .93 .94	1.0707 1.0641 1.0573 1.0505 1.0436
.20 .21 .22 .23 .24	1.9185 1.8729 1.8313 1.7933 1.7583	.45 .46 .47 .48 .49	1.3712 1.3610 1.3511 1.3416 1.3324	.70 .71 .72 .73 .74	1.1862 1.1806 1.1749 1.1694 1.1638	.95 .96 .97 .98 .99 1.00	1.0365 1.0294 1.0222 1.0149 1.0075 1.0000

录自 Zar JH:Biostatistical Analysis,p 574,Prenti-ce-Hall,Inc.,1974
统计量F值。

式中k为样本个数；Rj为各样本分别按式(10)计算的R值，其和为∑R_j;R为k个样本合并后求得的R值；N为各样本含量之和； 校正因子K仍由表4查出。当r=R/N在0.45以上时，式(12)较适用。求得F值后，查F界值表得P值，按所取检验水准作出推断结论。
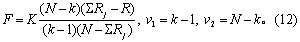
例8 比较表5中两组儿童心电轴(频数分别为f₁与f₂)的角均数。
H₀: μ₁＝μ₂
H₁: μ₁≠μ₂。α=0.05。

表5 两样本角均数的计算

心电轴(°) a	7～9岁组			10～13岁组
	f1	f1sina	f1cosa	f2	f2sina	f2cosa
-55 -10 10 30 50 70 90 110	1 1 2 13 31 53 24 4	-0.819152 -0.173648 0.347296 6.500000 23.747378 49.803709 24.000000 3.758770	0.573576 0.984808 1.969616 11.258330 19.926416 18.127068 0.000000 -1.368081	1 3 9 29 55 99 43 …	-0.819152 -0.520945 1.562834 14.500000 42.132444 93.029569 43.000000 …	0.573576 2.954423 8.863270 25.114737 35.353319 33.859994 0.000000 …
130 225				2 1	1.532089 -0.707107	-1.285575 -0.707107
合 计	129 (n1)	107.164353	51.471733	242 (n2)	193.709732	104.726637

按式(1)～(5)及式(10):　Y₁＝107.164353/129=0.830731,
7～9岁组　X₁＝51.471733/129=0.399006。

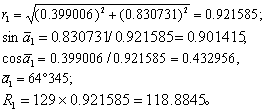
同理，10～13岁组
Y₂＝0.800453,
X₂＝0.432755。
r2=0.909946;
sinā2=0.879671,
cosā2=0.475583,
ā₂＝61°60;
R₂ =220.2069。
两组合并
∑sin ai=107.164353+193.709732=300.874085,∑cos ai=51.471733+104.726637=156.198370,
N=129+242=371,Y=0. 810981,X=0.421020。
r=0.913755,R=339.0031。
查表4，当r=0.913755时，经内插法K=1.0615，按式(11)得

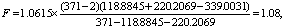
ν₁＝1,ν₂＝371-2=369，查F界值表得P>0.05。按a=0.05水准不拒绝H0，故认为两样本的角均数都估计同一个总体角均数，最佳估计值ā按(4)、(5)由合并数计算：
sin ā =0.810981/0.913755=0.88753,
或 cosā=0.421020/0.913755=0.46076。
ā=62.56°=62°34′。
两样本角方向的比较 用G.S. Watson非参数法，称为U2检验。检验假设H0为两样本来自角方向相同的两个总体。先将两组数据统一按大小排列，分组编秩，如表7第(1)、(2)、(4)、(5)栏，令i和j分别为样本1与样本2各角的秩号，a_1i为样本1的第i个角，a2j为样本2的第j个角；然后分别求两样本的累计频率，如表7第(3)、(6)栏，n₁与n₂分别为两样本含量，样本1的累计频率为i/n₁，样本2的累计频率为j/_n2；再求两累计频率之差d，如表7第(7)栏； N=n₁+n₂；统计量U²值的计算公式为

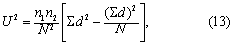
求得U²值后，查表6得P值，按所取检验水准作出推断结论。注意：同一P值时，Un1,n22=Un2,n12。例9 比较表7中两组儿童心电轴的角方向。
H₀: 两总体的角方向相同，
H₁: 两总体的角方向不同。
α=0.05。
N =11 +9=20,

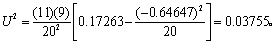
查表6得P>0.05，按a=0.05水准不拒绝H₀，故不能认为两的角方向不同。

表6 Watson检验用U²界值表

n1	n2	P		n1	n2	P
		0.05	0.01			0.05	0.01
4 4	4 5			5 6	30 6	.1802 .2060	.2419
4 4 4	6 7 8	.2167 .2273 .2361		6 6 6	7 8 9	.1941 .1964 .1926	.2821 .2976 .2617
4 4 4	9 10 11	.2436 .2018 .1949		6 6 6	10 11 12	.1896 .1872 .1829	.2479 .2620 .2593
4 4	12 13	.2031 .1855	.2604 .2647	6 6	13 14	.1849 .1839	.2497 .2506
4 4 4 4 4	14 15 16 17 18	.1931 .1807 .1836 .1839 .1818	.2685 .2719 .2750 .2778 .2481	6 6 6 6 6	15 16 17 18 19	.1852 .1823 .1833 .1840 .1832	.2487 .2500 .2472 .2461 .2498
4 4 4 4 4	19 20 21 22 23	.1796 .1842 .1819 .1823 .1814	.2517 .2451 .2486 .2517 .2394	6 6 6 7 7	20 21 22 7 8	.1824 .1834 .1824 .1986 .1817	.2490 .2475 .2473 .3036 .2722
4 4 4 4 4	24 25 26 27 28	.1797 .1814 .1816 .1786 .1775	.2411 .2441 .2396 .2360 .2388	7 7 7 7 7	9 10 11 12 13	.1818 .1866 .1839 .1855 .1842	.2552 .2622 .2532 .2519 .2523
4 4 5 5 5	29 30 5 6 7	.1794 .1797 .2250 .2424 .1998	.2369 .2395	7 7 7 7 7	14 15 16 17 18	.1840 .1845 .1848 .1827 .1841	.2530 .2503 .2508 .2500 .2502
5	8	.2154		7	20	.1832	.2499
5 5 5 5	9 10 11 12	.1909 .1956 .1901 .1863	.2798 .2889 .2969 .2608	8 8 8 8	8 9 10 11	.1836 .1863 .1852 .1842	.2500 .2582 .2491 .2524
5 5 5 5 5	13 14 15 16 17	.1837 .1820 .1835 .1825 .1820	.2692 .2571 .2515 .2552 .2472	8 8 8 8 8	12 13 14 15 16	.1854 .1853 .1855 .1855 .1854	.2521 .2531 .2516 .2507 .2531
5 5 5 5 5	18 19 20 21 22	.1797 .1824 .1824 .1810 .1820	.2464 .2526 .2416 .2448 .2426	9 9 9 9 9	9 10 11 12 13	.1867 .1860 .1845 .1852 .1850	.2663 .2538 .2552 .2540 .2526
5 5 5 5 5	23 24 25 26 27	.1811 .1810 .1810 .1806 .1804	.2451 .2437 .2461 .2447 .2443	9 9 10 10 10	14 15 10 11 12	.1843 .1850 .1850 .1856 .1848	.2526 .2541 .2545 .2548 .2545
5 5	28 29	.1802 .1802	.2417 .2443	10 ∞	13 ∞	.1853 .1869	.2542 .2684

摘自 Zar JH: Biostatistical Analysis,p 575,Pren-tice-Hall,Inc.,1974

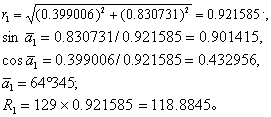
同理，10～13岁组
Y₂＝0.800453,
X₂＝0.432755。r2=0.909946;
sinā2 = 0.879671,
cosā2 =0.475583,
ā₂＝61°60;
R₂＝220.2069。
两组合并
∑sinai=107.164353+193.709732=300.874085,
∑cosai=51.471733+104.726637=156.198370,
N=129+242=371,Y=0.810981,X=0.421020。
r=0.913755,R=339.0031。
查表4，当r=0.913755时，经内插法K=1.0615，按式(11)得

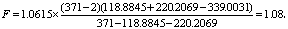
v₁＝1,v₂＝371-2=369，查F界值表得P>0.05。按α=0.05水准不拒绝H0，故认为两样本的角均数都估计同一个总体角均数，最佳估计值ā按(4)、(5)由合并数计算：sinā=0.810981/0.913755=0.88753,
或 cos ā=0.421020/0.913755=0.46076。
ā=62.56°=62°34′。
两样本角方向的比较 用G.S.Watson非参数法，称为U2检验。检验假设H0为两样本来自角方向相同的两个总体。先将两组数据统一按大小排列，分组编秩，如表7第(1)、(2)、(4)、(5)栏，令i和j分别为样本1与样本2各角的秩号，α_1i为样本1的第i个角，α₂j为样本2的第j个角；然后分别求两样本的累计频率，如表7第(3)、(6)栏，n₁与n₂分别为两样本含量，样本1的累计频率为i/n₁，样本2的累计频率为j/n₂；再求两累计频率之差d，如表7第(7)栏；N=n₁+n₂；统计量U²值的计算公式为

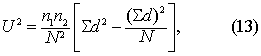
求得U²值后，查表6得P值，按所取检验水准作出推断结论。注意：同一P值时，U²_n1.n2＝U²_n1.n2,n12。
例9 比较表7中两组儿童心电轴的角方向。
H₀: 两总体的角方向相同，
H₁: 两总体的角方向不同。
α=0.05。
N=11+9=20,

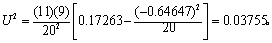
查表6得P>0.05，按α=0.05水准不拒绝H₀，故不能认为两组的角方向不同。

表6 Watson检验用U²界值表

n1	n2	P		n1	n2	P
		0.05	0.01			0.05	0.01
4 4	4 5			5 6	30 6	.1802 .2060	.2419
4 4 4	6 7 8	.2167 .2273 .2361		6 6 6	7 8 9	.1941 .1964 .1926	.2821 .2976 .2617
4 4 4	9 10 11	.2436 .2018 .1949		6 6 6	10 11 12	.1896 .1872 .1829	.2479 .2620 .2593
4 4	12 13	.2031 .1855	.2604 .2647	6 6	13 14	.1849 .1839	.2497 .2506
4 4 4 4 4	14 15 16 17 18	.1931 .1807 .1836 .1839 .1818	.2685 .2719 .2750 .2778 .2481	6 6 6 6 6	15 16 17 18 19	.1852 .1823 .1833 .1840 .1832	.2487 .2500 .2472 .2461 .2498
4 4 4 4 4	19 20 21 22 23	.1796 .1842 .1819 .1823 .1814	.2517 .2451 .2486 .2517 .2394	6 6 6 7 7	20 21 22 7 8	.1824 .1834 .1824 .1986 .1817	.2490 .2475 .2473 .3036 .2722
4 4 4 4 4	24 25 26 27 28	.1797 .1814 .1816 .1786 .1775	.2411 .2441 .2396 .2360 .2388	7 7 7 7 7	9 10 11 12 13	.1818 .1866 .1839 .1855 .1842	.2552 .2622 .2532 .2519 .2523
4 4 5 5 5	29 30 5 6 7	.1794 .1797 .2250 .2424 .1998	.2369 .2395	7 7 7 7 7	14 15 16 17 18	.1840 .1845 .1848 .1827 .1841	.2530 .2503 .2508 .2500 .2502
5	8	.2154		7	20	.1832	.2499
5 5 5 5	9 10 11 12	.1909 .1956 .1901 .1863	.2798 .2889 .2969 .2608	8 8 8 8	8 9 10 11	.1836 .1863 .1852 .1842	.2500 .2582 .2491 .2524
5 5 5 5 5	13 14 15 16 17	.1837 .1820 .1835 .1825 .1820	.2692 .2571 .2515 .2552 .2472	8 8 8 8 8	12 13 14 15 16	.1854 .1853 .1855 .1855 .1854	.2521 .2531 .2516 .2507 .2531
5 5 5 5 5	18 19 20 21 22	.1797 .1824 .1824 .1810 .1820	.2464 .2526 .2416 .2448 .2426	9 9 9 9 9	9 10 11 12 13	.1867 .1860 .1845 .1852 .1850	.2663 .2538 .2552 .2540 .2526
5 5 5 5 5	23 24 25 26 27	.1811 .1810 .1810 .1806 .1804	.2451 .2437 .2461 .2447 .2443	9 9 10 10 10	14 15 10 11 12	.1843 .1850 .1850 .1856 .1848	.2526 .2541 .2545 .2548 .2545
5 5	28 29	.1802 .1802	.2417 .2443	10 ∞	13 ∞	.1853 .1869	.2542 .2684

摘自 Zar JH: Bios tatistical Analysis,P 575,Pren-tice-Hall,Inc.,1974

表7 两样本角方向的比较(U²检验)

样 本 1			样 本 2			d=i/n1-j/n2 (7)=(3)-(6)	d2 (8)
i (1)	a1i(°) (2)	i/n1 (3)	j (4)	a2j(°) (5)	j/n2 (6)
1	-22	0.09091	…	…	0.00000	0.09091	0.00826
…	…	0.09091	1	-5	0.11111	-0.02020	0.00041
2	6	0.18182	…	…	0.11111	0.07071	0.00500
…	…	0.18182	2	26	0.22222	-0.04040	0.00163
3	38	0.27273	3	38	0.33333	-0.06060	0.00367
4	44	0.36364	…	…	0.33333	0.03031	0.00092
6	48	0.45455	4	48	0.44444	0.01011	0.00010
…	…	0.45455	5	56	0.55556	-0.10101	0.01020
6	58	0.54545	…	…	0.55556	-0.01011	0.00010
…	…	0.54545	6	59	0.66667	-0.12122	0.01469
7	70	0.63636	7	70	0.77778	-0.14142	0.02000
…	…	0.63636	8	74	0.88889	-0.25253	0.06377
8	77	0.72727	…	…	0.88889	-0.16162	0.02612
9	79	0.81818	…	…	0.88889	-0.07071	0.00500
10	82	0.90909	…	…	0.88889	0.02020	0.00041
11	86	1.00000	…	…	0.88889	0.11111	0.01235
…	…	1.00000	9	99	1.00000	0.00000	0.00000
n1=11			n2=9			-0.64647 Σd	0.17263 Σd2