因素分析yinsu fenxi

指一种多元统计分析方法。其目的是把一些具有错综复杂关系的因素归结为数量较少的几个综合因素（亦称共同因素），来解析事物的构成要素。因素分析方法有多种，计算过程也比较复杂，一般要借助于计算机的“因素分析程序”来完成。但其计算过程不外乎下面4个主要步骤：
一是根据原始资料求出各变量或项目之间的相关矩阵。如1984年从某省6万理科考生中随机抽取2千名考生，分别登记他们在数学试卷每题上的得分；然后把这些资料输入电子计算机求出这些考生在各题上得分之间的相关系数，就得到如下的相关矩阵。

表1 1984年高考数学（理科）各题间的相关矩阵

题号	1	2	3	4	5	6	7	8
1 2 3 4 5 6 7 8	1.000 0.392 0.396 0.284 0.283 0.349 0.255 0.090	0.392 1.000 0.459 0.378 0.390 0.466 0.345 0.078	0.396 0.459 1.000 0.396 0.280 0.459 0.292 0.068	0.284 0.378 0.396 1.000 0.270 0.370 0.231 0.048	0.283 0.390 0.280 0.270 1.000 0.349 0.329 0.130	0.349 0.466 0.459 0.370 0.349 1.000 0.326 0.122	0.255 0.345 0.292 0.231 0.329 0.326 1.000 0.039	0.090 0.078 0.068 0.048 0.130 0.122 0.039 1.000

这是一个对称矩阵，表中每个元素都是题间的相关系数rij。如r12=r21=0.392，表示第1题与第2题得分之间的相关；对角线上的元素为1，表示自身相关，余类举。
二是从相关矩阵中抽取适当数目的共同因素。由于因素分析的意图是用少数几个共同因素来代表或解析原来多个有关的因素。因此所抽取的共同因素不能太多，否则就无法达到因素分析的目的。
抽取共同因素的方法也有多种，如“形心法”、“主轴法”等。本文所采用的是“形心法”（亦称重心法），具体抽取因素的过程，可参阅叶佩华等人编著的《教育统计学》书第13章(人民教育出版社1982年)。借助于电子计算机的因素分析程序，不难从上面的相关矩阵出发，用“形心法”计得所抽取的因素矩阵(见表2)

表2 据表1所抽取的因素矩阵（未转轴）

因素 题号	因素Ⅰ	因素Ⅱ	因素Ⅲ	共同性(h2)
1 2 3 4 5 6 7 8	0.564 0.686 0.647 0.547 0.559 0.670 0.499 0.162	0.063 0.073 0.290 0.156 -0.289 0.044 -0.139 -0.119	0.093 0.113 0.033 0.081 0.064 -0.097 0.188 -0.158	0.331 0.489 0.504 0.330 0.400 0.460 0.304 0.065
平方和	2.543	0.2367	0.1029	2.883

上表中各个数字是因素负荷量，也是各题与这三个因素之间的相关系数。所谓因素负荷量是指某因素在某些项目（题目）上所承担的负载或所作出的“贡献”。例如，在表2中因素1在第1题上的负荷量为0.564，其平方为0.318，即称在第1题的单位方差中第Ⅰ因素所造成的方差占31.8%。表中“平方和”是某因素在各题上负荷量的平方之和；“共同性(h²)”是在某题上各因素负荷量的平方之和。
在表2中各个因素内的负荷量之间的差异不够大，使我们难以解释这些因素，因此需对表2的因素矩阵作转轴（或旋转）变换。
三是因素轴的旋转。旋转变换的目的是设法找到新的参照轴，使因素内部各负荷量之间的差异尽可能地大，使0或接近于0的负荷量的数目尽可能地多，这样就可使我们较容易地解释共同因素的含义。
因素轴的旋转方法有“直角转轴法”和“斜角转轴法”两种。转轴过程一般也是借助于电子计算机完成的。我们用“直角转轴法”中的“极大方差法”对表2的因素矩阵作旋转，得到下面新的因素矩阵(见表3)。

表3 旋转后的因素矩阵

因素 题号	因素Ⅰ	因素Ⅱ	因素Ⅲ	共同性(h2)
1 2 3 4 5 6 7 8	0.498 0.604 0.697 0.543 0.296 0.581 0.327 0.073	-0.286 0.351 -0.136 -0.155 -0.552 -0.306 -0.436 -0.139	0.031 0.038 0.020 0.110 0.083 0.169 0.080 0.202	0.331 0.489 0.505 0.331 0.399 0.460 0.303 0.065
平方和	1.931	0.855	0.097	2.883
百分比(%)	24.1	10.7	1.2	36.0

表中的“百分比”实质上是该因素负荷量之平方和的平均值（即平方和除以题目数），如第1因素各负荷量的平方和为1.931，其平均值为1.931/8=0.241，即24.1%。
四是因素的辨认和命名。在转轴后的因素矩阵里，因素内各负荷量之间的差异变大了，因而可以辨认某因素在哪些题目上有较高的负荷量。这些较高负荷量所对应的项目，就是该因素的代表项目；我们根据这些项目的内容及特征对该因素命一恰当的名字。这也是因素分析中最后要回答的问题。
从表3中可见：
❶在因素Ⅰ中以第2、3、4、6题的负荷量为大，它们所造成的方差占这个因素总方差的比重为76.8%，即

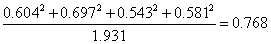
从命题说明及对试题的具体分析可知，这4道题主要反映了数学的基础知识、基本概念和基本运算，因而我们就把因素Ⅰ命名为“数学基础知识的能力因素”。从表中可知，该因素所造成的方差占整个试卷总方差的24.1%（百分比）。
❷在因素Ⅱ中以第5、7题的负荷量较大，这二题所造成的方差占该因素总方差的比重为

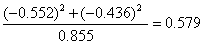
据有关专业知识可知：这二题主要反映了数学的计算能力和分析问题的能力，因而把这个因素命名为“数学计算与分析问题的能力”，这个因素所造成的方差占总方差的10.7%。
❸在因素Ⅲ中以第4、6、8题的负荷量较大，它们造成的方差占该因素方差的83.1%，即

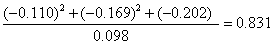
据当年命题说明可知，第4、6题主要考查几何中的空间想象能力，而第8题主要考查在代数中的逻辑推理知识，为此我们把这个因素命名为“空间想象和逻辑推理的能力因素”，而这个因素的方差占整个试卷总方差的1.2%。
通过上述因素分析结果可知：
❶原始资料反映了哪几个独立的共同因素；
❷这几个独立因素的主次顺序（依据它们占总方差的比重）怎样。从实例中的因素分析结果可知，1984年高考理科数学主要反映了3个独立的心理特征，它们的主次顺序是：基础知识与能力、计算与分析问题能力、空间想象与逻辑推理能力。但这3个独立的共同因素对总方差的贡献都偏低，说明该次考试并未充分反映这3个共同因素。

因素分析yinsu fenxi

一种统计技术。自1901年英国统计学家K·皮尔逊提出至今，其在理论上和方法上不断改进和创新，成为心理学家常用的一种统计技术。其中心任务是从一组变量或不同测验的实验数据中，找出其间潜含着的起决定作用的共同的基本因素。主要内容为：把n×n项的“相关矩阵”，通过一系列的数学处理，推导出一个由n×m (m

因素分析factor analysis

亦称“因子分析”。指研究多个观测变量(observed variables)之间的关系及结构的一种多元统计技术，旨在用较少数量的潜伏变量(latent vari-ables)即因素来解释各观测变量之间的关系。观测变量与因素之间的相关称为因素负荷(factor loadings)，范围由-1.00至+ 1.00之间的数值。因素负荷越大，越有意义，表示因素对观测变量的影响大。在应用因素分析技术时，研究者一般认为因素负荷应大于0.4或0.5才有意义。包括探索性因素分析(EFA)和验证性因素分析(CFA)两类。

因素分析factor analysis

亦称“因子分析”。从一系列变量中分离或抽取一些共同因素的多元分析方法。主要有两种基本形式： 探索性因素分析和验证性因素分析。前者致力于揭示事物的本质结构，主要用于理论模型的建立；后者主要用来检验已有的特定结构（即理论模型）是否按照预期方式产生作用，即用于验证理论模型。目的是用最少因素概括或解释最大量的观测事实，以最简洁概念揭示事物之间的本质联系，从而达到降维的效果。基本思想是依据变量间相关程度把变量进行分组，相关程度高的变量分为一组，相关程度低的变量分为不同组，然后用具有综合变量性质的共同因素来代表和解释每一组变量所蕴涵的基本结构。英国心理学家斯皮尔曼所提出的智力二因素理论是最早的因素分析理论，美国心理学家瑟斯顿在20世纪30年代发展出不同的因素提取方法，并提出智力多因素理论。随着计算机技术的发展、推广和普及，一些早期的抽取因素的方法被淘汰，主成分法、极大似然法、主轴因素法等成为主要的因素抽取方法。20世纪60年代发展的验证性因素分析，是通过研究获得的实际数据确定所假设的理论模型的各种参数，以期获得模型和数据的最佳拟合。在实际心理学研究中，因素分析的两种形式是综合在一起使用的，通过探索性因素分析建立模型，然后通过验证性因素分析验证理论模型。

因素分析

亦称“因子分析”。多元分析的一种。从一系列变量中分离或抽取一些共同因素的复杂统计分析过程。英国心理学家斯皮尔曼在研究智力结构时发展出来的一种统计方法。目的是用最少的因素来概括和解释最大量的观测事实，以最简洁的概念来揭示事物之间的本质联系。基本思想是根据变量间的相关程度大小，把变量进行分组，同组变量相关程度高，异组变量之间相关程度低，每组变量代表一种基本结构，然后用一个具有综合变量性质的共同因素来解释这个基本结构。