因子分析factor analysis

见“因素分析”。

因子分析factor analysis

多元统计分析的一个分支，用来研究一组指标的结构，其主要目标是降维，即降低用来刻画事物状态的指标的维数，以使对事物状态的描述更概括和简洁。在对实际问题进行研究时，把注意力集中于利用P个指标来构造几个不相关的具有最大方差的新指标，舍去那些 “贡献”很小的指标，从而降低所考虑问题中的指标的维数，使问题变得简洁。而因子分析方法则试图通过用最少个不可观测的变量 （即公共因子）来说明这些可观测的P个指标的相关模型，从而进一步简化模型。为了不失一般性，不妨假设X_i,i=1,2，…，p是零均值和单位方差的，方程式
X_i＝l_i1f₁+l_i2f₂+…+l_i3f₃+ε_i,i=1,2，…，P，其中被称为公共因子的f_k,k=1,2，…，s具有零均值、单位方差且互不相关； 被称为特定因子或“剩余”的ε_i,i=1,2，…，p也具有零均值、单位方差、互不相关；并且与f_k也互不相关。该方程式表示指标X的因子结构，其中系数l_ik在因子分析中被称为 “载荷”，相应的矩阵L=(l_ik) 称为载荷矩阵。h_k²＝l_1k²+l_2k²+…+l_pk²是公共因子f_k对X的总影响，或者说是f_k对X的贡献；g_i²＝l_1k²+l_2k²+…+l_ik²是X_i对公共因子的依赖程度，或者说是公共因子对X的“贡献”。因子分析的目的是要S比P小，而且尽可能选了小的S，以便提出一个简要的模型。在因子分析中要尽可能少地运用参数，这也称为软模型化 (soft modeling)这种方法用以建立社会经济学的模型。因为在社会经济学 (socioeconomic)分析中，因果链条上的每一个都只有很少的信息。因子分析最先用于心理学领域，在经济学方面的应用从斯通 (Stone,J.R.N.)的需求分析开始，至今已有不少应用成果，大多集中于经济发展方面。

因子分析

医学研究中经常遇到多指标的问题，例如描述牙槽弓形状特征可用22个指标。指标多会增加分析中的麻烦。事实上，不同指标之间往往有一定的相关性，因此有可能用较少的综合因子来代替原来较多的指标，使这些较少的因子既能综合反映原指标的大部分信息，而且相互之间可以是无关的。对于这些互不相关的因子，可以逐个地分析它所代表的意义。因子分析就是用以解决这类问题的。通常将p个指标X₁,X₂，…，X_p (简记为X_i,i=1,2，…，p)，综合而成的m个因子F₁,F₂，…，Fm(简记为Fj,j=1,2，…，m；且m≤p)。例如，按二个指标X₁,X₂测得n对数据，结果如图中散点所示。

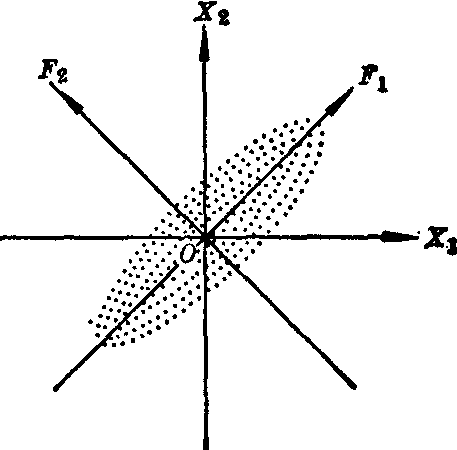
二指标因子分析示意

由图可见，这n个点子的分布有一定规律。这些点子的信息分别由X₁、X₂来反映，但X₁、X₂之间又显然有某种程度的相关，即X1增大时，X₂也增大。因此若用因子F₁、F₂来代替X₁、X₂，也就是用新坐标系F₁OF₂来代替
旧坐标系X₁OX₂，则不但可使F₁与F₂互不相关(F₂的大小与F₁的大小无关)，而且，因为这n个点大多沿着F₁轴散开，变异较大，而在F₂轴上则变异较小；故F₁就反映了X₁和X₂中所含的主要信息(比如说75%)。这样，只用F₁一个因子就能反映原来二个指标所含信息的75%，而F₂只反映全部信息中的25%，故称F₁为第一主因子，F₂为第二主因子。
原理 因子分析有二个基本问题：
(1)将指标用因子表达。

式中各F_j与所有的指标有关，称为公共因子，U_i(i=1,2，…，p)表示X_i中各Fj不能反映的部分，称为单一因子，后者只与对应的指标有关。因子分析的运算过程（可用计算机完成）就是按下述原则求各F_j的系数a_ij:❶各F_j之间互不相关，
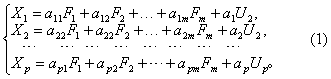
❷Fj的方差（用以反映指标的综合信息量）中，F₁的方差应最大，F₂的方差次之，依次递减。通常可用主成分分析法来求解。此时所求得的F₁,F₂，…，Fm又常称为第一、第二、…第m主成分。(2) 将公共因子用指标表达。式(2)的系数矩阵为式(1)中Fj的系数矩阵的转置矩阵。任一观察单位的各指标值代入式(2)就能求得各Fj值，它们可称为该观察单位的因子计量或因子得分，是从所有原始指标中，把与某一特定的因子有关的信息集中起来，必要时可利用因子计量作进一步的统计分析。
方法
(1)设有n个观察单位，各调查p个指标X₁,X₂，…，X_p，得数据排列如表1。

表1 p个指标的观察值

观察单位号	指 标
	X1	X2	…	Xp
1 2	X11 X21	X12 X22	… …	X1p X2p
…	…	…	…	…
n	Xn1	Xn2	…	Xnp

(2)将各Xi标准化，即各X_i分别减去其相应均数_i并除以其标准差s_i，记为x_i＝(X_i-_i) /s_i。 并求其两两相关系数，列成相关矩阵。由相关矩阵，用线性代数中的运算方法求得其p个特征根，从中选取m (m≤p)个λ_j (j=1,2，…，m)。并规定λ₁≥λ₂≥…≥λm，从而求得各λ_j的标准化特征向量l_ij。
(3)按式(3)计算式(1)中的a_ij

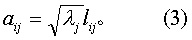
(4)计算所取的m个主因子F₁,F₂，…，F_m对某X_i的贡献V_i

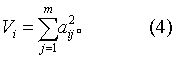
(5)式(1)中单一因子U_i的系数a_i，其平方值a²_i即为U_i的方差，可用下式求得。
a²_i＝1-V_i,(5)
式中a²_i表示m个主因子对指标X_i未能反映部分的信息量。
(6) 为使每一个公共因子只和最少数的指标有相关关系，必要时可进行因子旋转。
几个常用术语的意义：
(1)特征根λ_j体现了某一主因子F_j对所有指标X_i(i=1,2，…，p)总的贡献。因此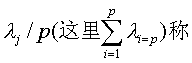，为主因子Fj的贡献率，即Fj所反映的是所有指标所含综合信息量的百分率。
(2)λj/p称为从F₁到F_m共m个主因子的累计贡献率，即m个主因子所反映的各Xi中所含综合信息的百分率。
(3) a_ij称为因子负荷量，它体现了某一主因子F_j对某指标X_i的贡献(即F_j反映X_i中所含信息的量)。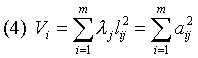是m个主因子F₁,F₂，…，F_m对某X_i的贡献。
因子分析分为R型和Q型两类。如上所述，从指标间的相关矩阵出发，提取指标中的主因子，称为R型分析。若从观察单位间的相关矩阵出发，提取观察单位中的主因子则称为Q型分析。在临床上，前者常用于对因子所代表的病因作分析和解释，后者可用于找主因子所代表的典型病例。
例 为了研究牙槽弓的形状特征，某单位调查了609例全口缺牙病人，每个患者各测22个指标Xi，分别反映上下牙槽弓的宽度、深度与长度。试用少数几个综合因子来概括这22个指标所反映的特征（本例仅考虑公共因子）。
(1)将各X_i标准化后，计算其两两间的相关系数，并由相关矩阵求出22个特征根及其累计贡献率见表2。

表2 累计贡献率的计算（节录）

因子Fj j	贡 献 λj	累计贡献 ∑λj	累计贡献率(%) ∑λj/22
1 2 3 4 5	10.2568 2.8334 2.1685 1.8811 1.2776	10.2568 13.0902 15.2587 17.1398 18.4174	46.62 59.50 69.36 77.91 83.72
⋮	⋮	⋮	⋮
22	0.0317	22.0000	100.00

(2)结合专业知识，可见仅取λ₁,λ₂与λ₃三个特征根其累计贡献率已近70%。这就是说仅取三个因子F₁、F₂与F₃就体现了原22个指标中所含信息的70%。由λ₁、λ₂与λ₃可计算得相应的标准化特征向量，见表3。

表3 三个主因子的标准化特征向量l_ij

由表2、表3按式(3)可求得各因子负荷量a_ij，见表4。

表4 因子负荷量及累计贡献率

指标	ai1	ai2	ai3	累计贡献率(%),Vi
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14 X15 X16 X17 X18 X19 X20 X21 X22	0.7209 0.7762 0.7788 0.7120 0.5431 0.6399 0.6862 0.6838 0.6709 0.5353 0.3861 0.6852 0.7039 0.4796 0.7592 0.7488 0.7588 0.7574 0.7598 0.7636 0.7020 0.5991	-0.1251 -0.1048 -0.0370 0.0344 0.1036 0.5652 0.6004 0.5521 0.4879 0.4076 -0.1113 -0.4769 -0.5205 0.3105 -0.1806 -0.2733 -0.4180 -0.4446 -0.1102 -0.1319 -0.1549 0.5077	0.0678 0.3054 0.4676 0.5626 0.5819 -0.2929 -0.0910 0.0822 0.1788 0.3229 -0.4197 -0.2173 -0.1254 -0.5560 -0.3424 -0.2758 0.0778 0.1162 -0.1043 -0.1137 -0.1051 -0.4054	53.98 70.67 82.65 82.46 64.41 81.47 83.96 77.92 72.01 55.68 33.76 74.42 78.21 63.56 72.62 71.15 75.66 78.48 60.03 61.34 52.78 78.10

表4中的a_ij即式(1)的系数矩阵的元素，其转置矩阵的元素即式(2)的各系数b_ji。

由表4及上式可见，F₁的各系数b₁i (i=1,2，…，22)均为正值且大小相近。这表示牙槽弓各指标的尺寸都大（即口型大）时，F₁也大；各指标都小（即口型小）时，F₁也小，故F₁可称为大小因子。F2的各系数b²_i有正也有负： X₆～X₁₀ （都反映下牙槽弓宽度）为正，X₁₁、X₁₂、X₁₃、X₁₅～X₃₁ (几乎全部深度、长度指标)为负。当前者较大，且后者较小时，则F₂值就大，表示下牙槽弓形状较扁平；反之，就较狭长，故F₂为反映下牙槽弓形状的形状因子。F₃的各系数b³_i也有正有负： X₁～X₅（都反映上牙槽弓宽度）为正，X₁₁～X₁₆ （反映上下牙槽弓深度）,X₁₉～X₂₂ （多反映下牙槽弓长度）为负。当F₃较大时，上牙槽弓形状扁平；反之则狭长，故F₃为反映上牙槽弓形状的形状因子。
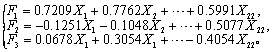
(3)据各因子负荷量a_ij，由式(4)可求得三个主因子对各X_i的累计贡献率V_i见表4最后一栏。由累计贡献率可见，取三个主因子时，对各指标的贡献已相当大，其中以对X₃、X4、X5、X₇、X、X₁₃、X₁₇、 X₁₈、 X₂₂的贡献较大，累计贡献率达75%以上，对其余的X_i (除X₁₁外)的贡献率也都在50%以上。

因子分析

把众多变量减少为含有一组相关的原始变量的少数因子的一种统计学分析。一个因子表示一系列数值的“负荷量”，它表明该因子与每一原始变量的相关水平。这样，一个因子便可解释高负荷量的原始变量，研究者即可对具有高负荷变量的特性进一步展开探讨和研究。每个因子仅仅是统计的产物，以某种计算机的程序表示了原始变量之间的相互关系。但因子本身常被看作是变量。它们的本质源于具有最高相关的原始变量的特性。例如，原始变量可以是157个联合国成员国在100个国际问题上的投票行为，这样，投票数可由一个100个垂直栏目和157个水平栏目的表格表示。运用因子分析，可以有效地将栏目数由100个减少到12个左右，新栏目表示对每一国家拥有一个数值负荷量的因子，而每一数值负荷量又表示与某个特殊水平或特殊因素相关的某国投票行为的机率。如果高负荷量的国家都是西欧国家，则可贴上“西欧”水平标签，而别的因子也可能仅对东欧国家显出高负荷量；另一因子则可能表示了另一些没有明显的共同特征的国家。因子分析只是显示了这些统计关系；对这些关系的解释还需人们的进一步研究。因子分析的主要优点是能把大量资料和数据减少成容易处理的几个部分，并提出不太明显的变量之间的关系的假设。

因子分析factor analysis

最初由斯皮尔曼(Spearman,C.)1904年提出。这是一种多元统计分析方法，其目的是为了减少用于描述事物状态的指标的维数，从而易于概括出该事物的本质。例如，在用p个指标X_i(i=1,2，…，p)描述事物的状态来研究一组指标的结构时，可以通过用尽可能少的且不可观测的变量（公共因子）来描述这些可观测的p个指标的相关模型，以便减少所考虑问题中的指标维数。
设有方程式：X_i＝C_i1Z₁+C_i2Z₂+…+C_isZ_s+ε_i表示指标X的因子结构。
其中：X_i(i=1,2，…，p)具有零均值、单位方差；
Z_k(k=1,2，…，s)为公共因子，具有零均值、单位方差、互不相关；
C_ik(i=1,2，…，p k=1,2，…，s)称为“载荷”；
ε_i(i=1,2，…，p)为特定因子，具有零均值、单位方差、互不相关，并且与Z_k也互不相关。
假定公共因子Z_k对X各分量的总影响是：D_k²＝C_1k²+C_2k²+…+C_pk²,X_i对公共因子的依赖程度为：E_i²＝C_i1²+C_i2²+…+C_ik²。
因子分析就是要选取一组公共因子Z_k(k=1,2，…，s)，使得Z_k的个数小于变量X_i(i=1,2，…，p)的个数，即s

有关因子分析的理论和模型目前还不是很完善。比如，载荷矩阵C=(C_ik)不具惟一性，它可用矩阵CM替代(M是正交矩阵)。这就需要在实际中选择合适的M，来简化因子结构，以便能更好地解释其结果。
因子分析应用广泛，在心理学、经济学、医学、农业和其他社会科学领域都有很好的应用。