σ－空间与Σ－空间

---

自1944年丢当内(Dieudonné)定义仿紧空间以后，对仿紧性理论的研究蓬勃开展，主要是由于它包含著度量空间与紧空间两大空间类。

它的弱点是两个仿紧空间的积未必是仿紧的。为了使仿紧空间的积保持仿紧性，必须加上某些条件。

下面叙述可数个仿紧空间的积的情况。这一问题可以归结为找出这样的空间类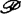(尽可能广泛些)，使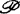中仿紧元素序列的积是仿紧的。对类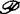本身来说也要求关于某些通常的拓扑运算是封闭的。在这一方面已取得了相当满意的结果。

1960年福罗立克(Frolik)把类p取为所有岂赫(Cech)意义下完备拓扑空间。1963年阿尔亨格尔斯基(Arhangel’skii)推广福罗立克的研究结果，把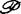取为所有p空间的类(按岂赫意义下完备空间是p空间)。

1964年森田纪一(Morita)得到等价的结果，把p取为所有M空间类。M空间不同于p空间，但仿紧M空间类与仿紧p空间类是重合的。从完全不同的方向，奥山晃弘(Okuyama)于1967年取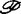为σ－空间类。1969年永见启应(Nagami)取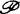为Σ－空间类统一地推广了前面的所有结果。

σ－空间与Σ－空间不仅在仿紧空间的可数积保持仿紧性这一问题上起著重要作用，致使仿紧空间的应用更广泛，而它们本身也都是度量空间在某些方面的推广，且具有良好的性质，甚至比度量空间更良好的性质(下文σ－空间及Σ－空间的性质(5))，从而决定著它们在拓扑空间理论中的重要地位。

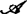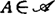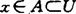空间X的子集族称为这空间的网，如果对每开集U及x∈U，存在，使，如果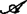是σ－离散、σ－局部有限、σ－闭包保持、或σ－遗传性闭包保持的，则称这网是σ－离散、σ－局部有限、σ－闭包保持、或σ－遗传性闭包保持的，如果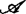是闭集族，则称这网是闭网。

空间X称为σ－空间，如果它具有σ－局部有限闭网，按此定义，无非是把著名度量化定理中的基底换为网(基底的元素必须是开的，网则不然)，对正则空间X，下列性质是等价的：
❶ X具有σ－离散网，
❷ X是σ－空间，
❸ X具有σ－闭包保持网。

σ－空间具有下列良好的性质：
❶ 在正则空间，σ－空间在闭映射下的象是σ－空间。

❷ 设｛X_n｝是σ－空间是序列，则积空间П(X_{n∶n=1，2，……}｝是σ－空间。
❸ 设｛X_n｝是仿紧σ－空间的序列，则积空间П｛X_{n∶n=1．2，……}｝是仿紧σ－空间。

❹ σ－空间的任何子空间是σ－空间。
❺ 设空间X是可数个闭σ－子空间的并，则X是σ－空间。

❻ 设空间X具有局部有限闭复盖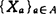，每一X_a(σ∈A)是σ－空间，则X是σ－空间，
❼ 设X是正规空间，X为闭复盖｛X_a｝_a∈A所控制，每一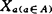是σ－空间，则X是σ－空间(按X为闭复盖所控制是较弱于这闭复盖是局部有限的情况)。

以上性质是奥山晃弘在1967～1971年得到的，性质❼ 中的条件“正规”能否去掉?直到最近(1991年)才为林寿肯定地解决。

空间X称为半分层空间，如果对X中每一开集U，可以确定一闭集序列｛Un｝满足：(1)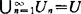，(2)设U、V是开集，且U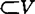，则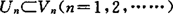；如果更满足(3)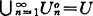，这里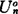是U_n的内核，则称X是分层空间，分层空间是σ－空间，σ－空间是半分层空间。分层空间、半分层空间都具有比较良好的性质。

特别分层空间是正规且仿紧的，它具有相应于σ－空间的性质：
❶ 、❷ 、❸ 、❹ 、❻ 、❼ 。

σ－空间类已解决了所提出的可数个仿紧元素的积是仿紧的问题(见上述σ－空间的性质❸ )，但是仿紧σ－空间类与仿紧M空间类(或仿紧p空间类)设有什么“联系”，更不能包含对方。

永见启应引入的Σ－空间类既解决了可数个仿紧元素的积是仿紧的问题(见下面Σ－空间性质(3))，又能同时包含σ－空间类与M空间类。

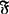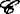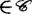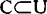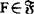空间X称为Σ－空间(强Σ－空间)，如果存在σ－局部有限闭集族及由可数紧集(紧集)组成的复盖使对X中的开集U，C，，存在使。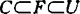

显然σ－空间→强Σ－空间→Σ－空间。

由上述定义，易知σ－空间按完备映射(闭映射且每一纤维是紧的)的原象是强Σ－空间，按准完备映射(闭映射且每一纤维是可数紧的)的原象是Σ－空间，但其逆均不真，后者均严格地包含前者。

Σ－空间(强Σ－空间)具有下列良好的性质(便于读者比较，按σ－空间的相应性质的次序排列)：
❶ 设f是空间X到空间Y上的准完备映射，则X是Σ－空间当仅当Y是Σ－空间，
❷ ’设｛X_n｝是强Σ－空间的序列，则积空间П｛X_n：n=1，2，……｝是强Σ－空间。
❸ 设｛X_n｝是仿紧Σ－空间的序列，则积空间П｛X_n：n=1，2……，｝是仿紧Σ－空间。

❹ Σ－空间的F_σδ子空间是Σ－空间。
❺ 设空间X是可数个闭Σ－子空间的并，则X是Σ－空间。
❻ 设空间X具有局部有限闭复盖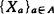，每一X_a(a∈A)是Σ－空间，则X是Σ－空间。
❼ 设空间X为闭复盖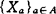所控制，每一X_a(a∈A)是完全正规的Σ－空间，则X是Σ－空间。

以上性质是永见启应于1969年得到的。其中性质❷ ′是对强Σ－空间说的，不是对Σ－空间说的。

显得很不协调，故用❷ ′表示。是否可将❷ ′中的“强Σ－空间”都换成“Σ－空间”?这问题尚未解决。

又性质❼ 中的条件“完全正规”能否去掉?至今尚未解决。

至于怎样的Σ－空间才是强Σ－空间?有：“空间X是强Σ－空间当仅当它是次仿紧的Σ－空间”。

怎样的Σ－空间才是σ－空间?有：“空间X是σ－空间当仅当它是具有G_δ对角线的Σ－空间”。

比较σ－空间与Σ－空间的性质❶ ，前者为闭映射所保持，后者为准完备映射保持。

后者对映射性质的要求较强。是否Σ－空间也能为闭映射保持?答案是否定的。为此学者们引入Σ^*－空间⁽Σ#-空间)以推广Σ－空间且使能为闭映射所保持。

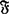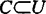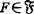空间X称为Σ^*－空间(Σ^#－空间)，如果存在σ－遗传性闭包保持(σ－闭包保持)闭集族及由可数紧集组成的复盖c使对X中开集U及C∈c，，存在使。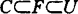

这里是把Σ－空间定义中的“局部有限”分别改为“遗传性闭包保持”及“闭包保持”，由于局部有限→遗传性闭保持→闭包保持，所以Σ－空间→Σ^*－空间→Σ^#－空间。其逆均不真。

由上述定义可知Σ^*－空间、Σ^#－空间在闭映射下的象分别是Σ^*－空间、Σ^#－空间。这样对空间的映射性质改善了，可是对积空间的保持却不那么“良好”了。

奥山晃弘指出，如果X是仿紧Σ^*－空间而不是Σ－空间(麦考尔(Michael)曾作出这样的空间以说明Σ－空间不能为闭映射所保持)，则X与闭区间的积不是Σ^*－空间。Σ^#－空间的情况较好些，奥山晃弘证明：“Σ^#－空间与紧空间的积是Σ^#－空间。麦考尔指出，Σ^#－空间在拓扑空间理论中的应用取决于下述关键性问题：“如果X、Y都是仿紧Σ^#－空间，X×Y是否一定是仿紧空间?”这问题尚未解决。

为了说明Σ^#－空间与σ－空间的关系，下面引入σ^#－空间：空间X称为σ^#－空间，如果存在σ－闭包保持闭集族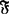，使对每一x∈X，。

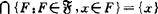利用这概念，我们有：“下列性质是等价的：
❶ X是σ－空间；
❷ X是Σ－空间及σ^#－空间；
❸ X是Σ^#－空间及σ^#－空间。”。

。【参考文献】：

1 Frolik Z. BullAcad Polon Math Ser,1960,8:747～750

2 Arhangel'skii A V. SSSR 1963,151:751～754

3 MoritaK. Math Ann, 1964,154:365～382

4 Okuyama. Sci Rep Tokyo Kyoiku Daigaku Sec. A,1967,9: 236～254

5 Michael E A. Proc. Wash,Stote Univ Conf Gen Top, 1969, 13～19

6 Nagami K. Fund Math, 1969,65:160～192

7 Okuyama A. Pacific J Math, 1972,42:485～495

8 高国士．σ－空间、Σ－空间及Heath-Hodel映象(上)，1984，4∶137～142

9 林寿．数学年刊，1991，12A：186～189

(苏州大学高国士教授撰)

上一篇：保圆几何
下一篇：光滑映射芽的决定性理论

"σ控制图σ控制图

---

一译“标准差控制图”。

控制图的一种。在于表征一个过程的质量特征X，且要求把它的标准差控制在σ₀水平上时，若以样本标准差S作为被控制的样本特征建立起来的3σ控制图。

S是总体方差σ的无偏估计。控制图中心限是E(S)，上、下控制限为E(S)+3σ_s与E(S)－3σ_S，其中E(S)是S的均值，σs是S的标准差。

参见“3σ控制图”。