T2统计量

---

服从T²分布的统计量。

霍德林1931年给出。设Y和W是独立的，且Y～N_p(μ，∑)，nW～W_p(n，∑)，则T²=Y′W^－1Y所服从的分布，称“非中心T²－分布”，T²称“T²统计量”。

常简记为T²～T²(p，n，δ)，(0≤T²＜+∞)，式中非中心参数δ=μ′∑^－1μ。在μ=0时，δ=0，此时T²为中心T²分布。

有人将T²统计量称为“HotellingT²统计量”。威忌斯曼和博克研究了T²统计量与F统计量之间的关系，取得如下成果：设T²=Y′W^－1Y，此处Y～N_p(μ，∑)，nW～W_p(n，∑)，且Y与W彼此独立，则有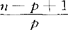·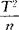～F(p，n－p+1，δ)，即T²可转化为F分布。

此处F的自由度是p与n－p+1，非中心参数δ=μ′∑^－1μ。在多元分析中，杰森和荷伟1968年编制了T²统计量的上侧百分位点的数值表以供查阅，也可转为F分布，查阅F统计量的数值表。T²分布在多维正态分布的均值检验中有著直接应用。

如为检验H₀：μ=μ₀；H₁：μ≠μ₀。从p维正态总体Y中随机抽取样本Y₁，Y₂，…，Y_n，即有Y_i～IN_p(_μ，∑)(“IN”表示彼此独立的正态变量)，于是Y～N_p(μ，∑／N)，(N－1)S～W_p(N一1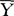，∑)，与S也相互独立。构造检验统计量T²=N(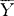－μ₀)′S^－1(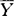－μ₀)，在H₀成立时，T²服从T²(p，N－1)分布，或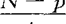·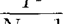服从F(p，N－p)分布(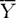是样本均值向量，S是样本方差－协方差矩阵)。