参数估计parameter estimation

由总体抽得的样本估计该总体的未知参数的统计推断方法，可分为参数的点估计和区间估计。
参数的点估计 用样本的特征数估计总体相应的特征数，其常用方法有矩估计法和极大似然法两种。
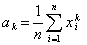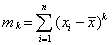矩估计法 用样本的r阶矩作为总体的r阶矩的估值。设x₁,x₂，…，x_n是容量为n的样本，k为自然数，分别称和为k阶样本原点矩和k阶样本中心矩，统称为样本矩。设总体X的分布函数为F(x),k为任一正整数，分别称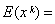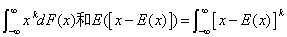dF(x)为总体X的k阶原点矩分别是它的数学期望μ和方差^σ2，所以可用一阶样本原点矩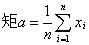和二阶样本中心矩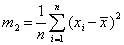分别来估计总体均值μ和方差^σ2
极大似然法 设总体X的分布是连续的，其密度

(i=1、2、…、k)，就可以确定所求的θ₁、θ₂、…、θk值。如果总体的分布是离散型的，只要把上述似然函数中的密度函数f(x_i,θ₁、θ₂、…、θk)用分布列P(X=x_i)代替就可以了。对于某正态总体的未知参数μ和σ²，可根据该总体的n次观察值x₁、x₂、…，x_n来求它们的最大似然估计值。因为总体的分布密度函数为
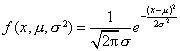
因此，似然函数为

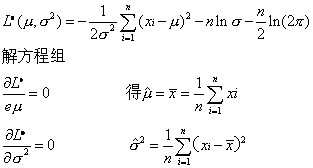
分别为μ与σ²的极大似然估计值。
可用来估计参数θ的估计量很多，因而产生了估计量的优良性问题，这种优良性的标准不是唯一的，可以根据问题的实际背景和应用方便进行选择，主要包括参数估计量的无偏性、有效性和一致性。
如果参数θ的估计量θ满足关系E(θ)=θ，则称θ是θ的无偏估计。
若θ1和θ₂都是θ的无偏估计，且两者的方差比
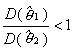
则称θ₁比θ2有效。如果固定样本容量n，使D(θ)=极小值的无偏估计值，θ就称为θ的有效估值。
若样本容量n趋向无穷大即n→∞时，θ→θ，则称θ是θ的一致估计量。
参数的区间估计 由总体抽得的样本来估计在一定概率保证下包含总体参数θ的区间[_L1、L₂]的统计推断方法。保证参数θ在该区间的概率P=1-α(农化研究中α常取0.05和0.01)称为置信概率或置信度。这个区间[_L1、L₂]称为θ的1-α置信区间，其中L₂、L1分别称为置信上限和置信下限，统称为置限。正态总体的均值μ的1-α置信上、下限列于下表，表中
数，可查正态分布和t分布表得到（见抽样分布）。

正态总体均值μ的1-α置信上、下限表

参数估计

由样本(Z₁,Z₂，…，Z_n)对总体分布F(x;θ)中的未知参数θ进行估计的方法。是统计推断的基本问题之一。分为点估计和区间估计两类。在实际工作中，已知或由大量累计资料可以确定研究总体的分布类型，但分布参数未知，或者人们只关心分布中某些数字特征，这就需要由有限样本来估计未知参数，从而掌握总体分布特征。如评价产品的平均质量指标，质量波动程度，两批同类产品的质量对比，同地区某一指标的对比及总体比例(如产品的合格率，返修率，出生率)等方面，有些不能采用普查方法，同时为了省时省力而采用随机抽样方法，用样本资料对其真值进行估计。常被应用于测验分数统计中。

参数估计canshu guji

通过样本的信息对有关总体参数的情况进行推估。包括点估计和区间估计。
点估计是用样本统计量的一个具体值来估计相应的总体参数。如在一个样本中，可得出一个样本平均数＝60，用它作为总体平均数μ的估计值；当然它不一定刚好等于μ，但希望尽量接近于μ，因此＝60就是μ的点估计。可见点估计是一种不大精确的估计。如果取多个样本统计量的平均值来估计总体参数，则要准确得多；如μ＝μ,μs²＝σ2等。但取多个样本较耗时费力。
区间估计是在一次抽样中以某种样本统计量来估计相应总体参数时，用较大的概率（称为置信度）来保证这种估计。例如在一个容量为36的样本中计得＝56，则它相应的总体参数μ不一定刚好为56，而是在56附近的某个区间内。由于μ是未知的，我们只能以较大的概率(如95%)来保证μ落在56附近的某个区间内。这个区间就称为置信区间。其步骤是：
❶确定统计量的抽样分布服从何种分布。如前面已知当n较大时的抽样分布服从于正态分布。
❷确定统计量的标准误。如的标准误为SE＝S/,n为已知，S可在样本中计出(假定S=10)。
❸确定置信度P或置信水平(小概率a=1—p) 一般p取0.95 (a=0.05)或0.99 (a=0.01)。
❹在统计量所服从的分布中找到a/2与(1—a/2)的界限值，如设a=0.05，则在正态分布表中可查到，Za/2=-1.96,Z(₁-σ_/2)=1.96。
❺据下面表1的有关公式写出样本统计量的估计相应总体参数的置信区间。本例中可知，X估计μ的置信区间为[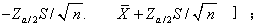
；把上述各数值代入此区间即得[52.08,59.92]。这就是说.我们以95%的把握估计μ落在[52.08,59.92]内；或者说，μ落入[52.08,59.92]的概率为0.95.

表1 一个总体的主要参数估计一览表

注：p为比例或百分比，r为相关系数，Zr是r对z的转换值。
[例1] 从某市初中毕业生中随机抽取1000名学生，测得他们的近视率为25%。利用表1中关于比例的置信区间公式可求得(设α=0.05)该市初中毕业生总体的近视率为：

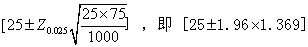
故以95%的把握推断该市初中毕业生总体的近视率在22.3～27.7%之间。

表2 关于二个总体的主要参数估计一览表

[例2] 为调查某市中学生体育锻炼达标情况，随机抽查男生2500人中有1 300人达标，女生1800人中有1 100人达标。试对全市中学男、女生达标率之差异做出估计(取α=0.05)。
在表2中找到关于两总体率π₁-π₂的置信区间公即[0.06,0.12]。这就是说，在样本中它们相差0.09，而在总体中它们差异是在0.06～0.12之间，而且是以95%的把握作出这一估计的。

参数估计

数理统计的一个重要内容。见“非参数统计”。

参数估计Parameter Estimation

统计推断的一种基本形式。根据从总体中抽取的样本估计总体分布中包含的未知参数的方法。分为点估计和区间估计。

参数估计

利用有关的方法，在实际观测数据的基础上求得经济计量模型的参数所进行的计算。参见“经济计量模型”。

参数估计

运用样本数据对总体参数值作出估计。是统计推断中的一项基本内容。例如，要了解某市职工对住房改革的满意程度，通常用抽样调查所得到的样本平均值、标准差和百分比等统计值来估计全市职工这一总体的平均值、标准差和百分比等参数值，这就是参数估计。参数估计可分为点估计和区间估计。点估计又称定值估计，即以实际抽样调查资料得到的抽样指标值作为总体指标的估计值，同时给出极限误差和相应的可靠程度。区间估计是根据估计可靠程度的要求，选定概率度t，以及极限误差△x=tμx，再利用抽样调查取得的抽样平均数, 定出估计上限+△x和估计下限-△x。区间(-△x,+△x)称为置信区间，估计可靠程度为置信度。区间估计就是根据抽样指标定出置信区间和置信度。参数估计除了用样本平均数()来估计总体平均数μ外，还可用样本比率 (p) 来估计总体比率(P)。参数估计有许多方法，如矩估计、最大似然估计、贝叶斯估计、顺序量估计及最小二乘法估计等。

参数估计parameter estimator

在已知总体分布的条件下，利用样本信息对总体数字特征进行统计推断的过程。常用于统计分析和企业产品质量控制、估计计量经济模型的参数等方面。参数估计分点估计和区间估计两种。

参数估计

统计上常用参数来描述总体的特征，如用总体均数、中位数和众数等来描述总体的中心位置或集中趋势； 用总体标准差、极差和四分位数间距等来描述总体的离散度。但总体参数常属未知，而需进行参数估计，也就是用样本统计量来估计总体参数（包括其估计误差）。参数估计和假设检验是统计推断的两个重要领域。
参数估计分为点估计和区间估计。点估计是给出被估计参数一个适当的估计值； 区间估计是给出被估计参数的可能的数值范围。如抽样调查某地7岁男孩身高，得样本均数119.1cm，以此作为该地7岁男孩身高总体均数的估计值，这是点估计。若提出该地7岁男孩身高总体均数的95%可信区间为118.3～119.9cm，这是区间估计。在科技报告中，点估计与区间估计常同时写出，如本例可写成： 119.1cm (118.3,119.9cm)。用点估计时，为了说明估计的精度，常同时写明标准误。

参数估计

又称“抽样估计”、“母数估计”。推论性统计的一项基本内容，是用样本统计值来估计总体参数值的一种统计方法。例如，要了解某市居民对住房分配的满意程度，通常用抽样调查所得到的样本平均值、标准差与百分比等统计值来估计全市居民这一总体的平均值、标准差与百分比等参数值。参数估计可以分为点估计和区间估计。点估计是直接用样本统计值来估计一个单一的总体参数值，所以又称单值估计。点估计不考虑随机变量的抽样误差和概率分布，因而不能反映估计的参数与真正的总体指标有多大的误差以及估计的可靠程度。例如，假定上例中真正的总体指标是全市居民中42%的人对住房分配不太满意，但调查的样本统计值为40%，由于并不知道真正的总体指标为42%，所以不知道估计的参数与真正的总体指标有2%的误差。又假如从同一总体中抽样调查的另一个样本统计值为38%，那么究竟把哪一个统计值作为总体参数值是可靠的呢？所以点估计无法反映估计的误差和可靠程度。区间估计是以数值的区间形式来确定总体参数的可能范围。它根据概率抽样的理论，以一定的概率即可靠程度来保证真正的总体指标落在某一区间内。例如，假定上述对某市居民住房问题的调查，抽取的样本统计值表明，该样本中有40%的居民对住房不太满意。如果这次抽样是在95%的概率保证下进行的，其最大抽样误差为3%，这时就可以说，该总体真正的参数落在40%±3%的区间内，即全市居民有37%至43%的人对住房分配不太满意，这一结论有95%的可靠程度。在舆论调查中，参数估计主要用于两种情况：(1)用样本平均数()来估计总体平均数(M);(2)用样本比率(P)来估计总体比率(p)。上例就属于用样本比率来估计总体比率。区间估计中，以一定的概率即估计的可靠程度来保证总体参数落在某一区间内，这一区间的两个极端值不会超过允许的误差范围，这种情况下的概率即估计的可靠程度就称为可信度、置信度、可信系数或置信系数；这样的区间即为所需估计参数的可信区间或置信区间。如上例中95%的概率即为这次估计的可信度，参数值落入的区间(37%至43%)即为这次估计的可信区间。

参数估计

通过样本指标来推算总体参数的方法。是统计推断的重要内容。例如根据样本平均数和样本方差S², 估计总体平均数μ和总体方差σ2。样本平均差和样本方差称为统计量，总体平均数和总体方差称为总体参数。参数估计有点估计和区间估计两种。当用样本指标去估计总体指标时，如果将样本指标作为总体参数θ的估计值， 要求满足E()=θ。 满足这个条件的样本指标， 即为总体参数θ的无偏估计量。 设、 ₁是θ的两个无偏估计量， 如果比₁更密集在θ附近， 就认为较理想； 若满足E()=θ, 且除以外对θ的其他估计量₁，均有D(₁)≥D(), 则称是对θ的最有效估计量。参数估计有许多方法，如最大似然估计法、最小二乘法等。

参数估计parameter estimation

统计推断基本形式之一。通过样本统计量对总体参数进行估计的统计方法。总体参数未知，从总体中随机抽取一个样本，根据样本分布规律求得总体参数。主要包括点估计和区间估计两种。

参数估计

通过计算样本的统计量，对样本所属总体的参数作出估计的统计方法。常用方法有点估计和区间估计。