单纯形法

求解具有有限个决策变量的线性规划数学模型的方法。是一种迭代方法，如目标函数值还有可能进一步改善，则从一个初始可行基本解出发，重复求解过程，经过有限次可求出最优解。

单纯形法simplex method

最简单的线性规划问题约束条件与角点为数不多，可用代数法求解；对比较复杂的、大型线性规划问题一般采用单纯形法，利用计算机求解。所谓单纯形法，从根本上说，是一种从可能解区的一个隅角点转移到另一隅角点的逼近法；每前进一步就能达到一个较大的目标近似值。这方法保证在有限的步伐内求得最佳解。

单纯形法

从满足由所有有限资源构成的约束条件的可行方案中，用方案替代法逐步找到使目标函数达到最大 （或最小） 值的一种优化方案的计算方法和步骤。它是线性规划问题的通用解法，由丹捷格于1947年首创。基本思路是： 先将线性规划模型变为标准型，然后从一个可行基出发，通过逐步迭代，不断改进得到最优解。这里规定标准型为：
目标函数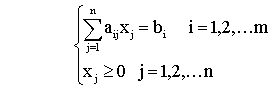

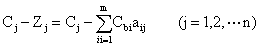
用单纯形法求解线性规划问题，一般都需要借助电子计算机进行。现举例说明计算方法和步骤如下：
目标函数 MaxZ=30x₁+40x₂+20x₃

第一步： 在上述线性规划问题的约束条件中分别加入松弛变量x4、x5、x6，使之变为标准型。确定x4、x5、x6的初始基本可行解，对应的单纯形表见表1。从表1中可看到初始解中基变量x₄、x₅、x6的取值分别是b列中的20、30、20，其他变量x1、x2、x3都应等于零。检验数按下列公式计算：

表中分别计算得到：

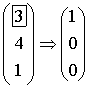
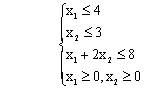
C₁-Z₁＝30-(0×3+0×2+0×6) =30C
₂-Z₂＝40-(0×3+0×4+0×1) =40C
₃-Z₃＝20-(0×1+0×3+0×1) =20

其他的都是零。

表1 初始单纯形表

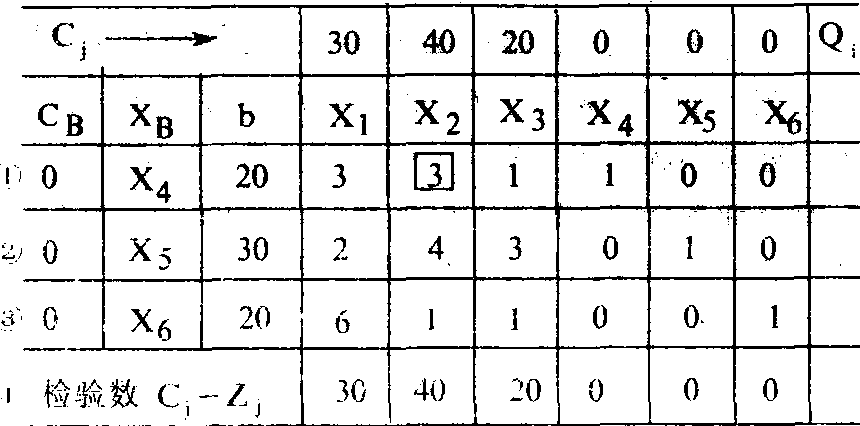
第二步： 检查所有检验数是否都小于或等于零。若是，已得到最优解，则停止计算。否则转入下一步。本例中的检验数都大于零，要进行下一步运算。
第三步： 检查所有大于零的检验数所在列中数字是否都是非正的。若有，则此问题无解，可停止计算。若无，则转入下一步。本例应转入下一步运算。
第四步： 从所有大于零的检验数中找出最大的数，它所在列的那个变量，确立为换入变量。本例是确立Max (30,40,20) =40，它所在列的X2为换入变量。再按最小比例规则 (Q规则) 计算。

确定Q所在行的变量Xi为换出变量。本例中

它所在行的变量是X4，确立X4是换出变量，a12=3是主元素，给一个标志□，以示注意。转入下一步运算。
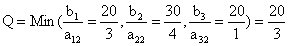
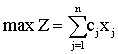
第五步： 在另一个新表 (表2) 中进行基变量变换运算，可用高斯消元法或矩阵初等变换把X2所在列的各元素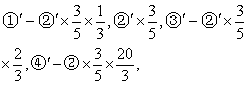本例中表2的各行的系数的运算步骤分别是❶/3,
❷-❶/3×4,
❸-❶/3×1,
❹-❶/3×40 (❶,
❷,
❸,
❹代表原表 (表1) 第❶、
❷、
❸、
❹行的各个对应系数) 。例如，求新表第2行b的数字，则是30-20/3×4=10/3。如此类推。再将初始表中XB列中的X4换成X2，得到新表 (表2)。再以表2为起点重复第二步的判断。确立X3为换入变量。计算Q，确定X5为换出变量，进行迭代，下表3第❶”、
❷”、
❸”、
❹”行的系数的计算步骤为：

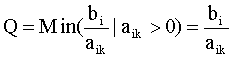
于是得到最终计算表(表3)。
表2

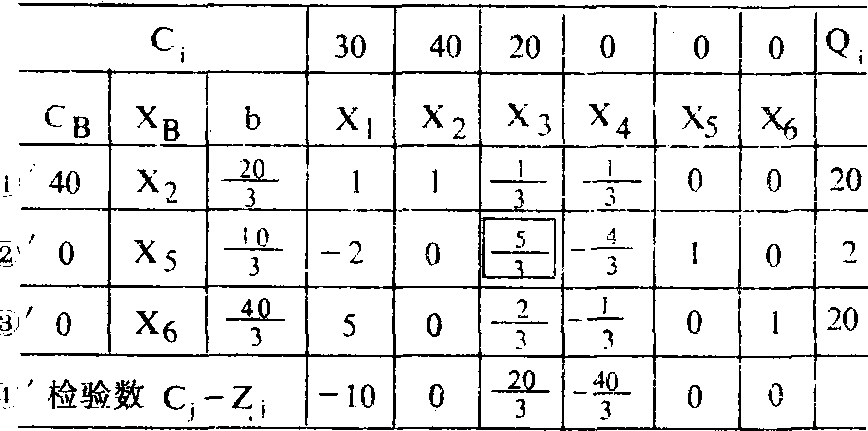
表3

从最终计算表中可见所有检验数都小于或等于零。故已得最优解： X2=6,X3=2,X6=12,X1=X4=X5=0。将它们代入目标函数得到Z=280。
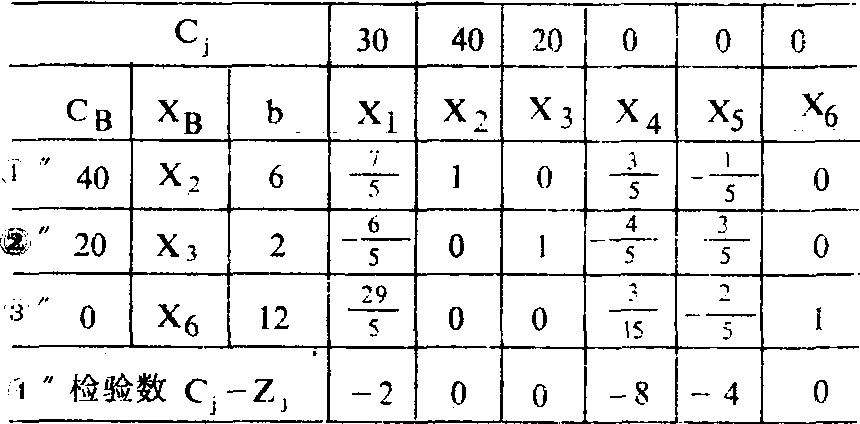
对于本身不存在最优解或存在特殊最优解的线性规划问题，用单纯形法计算时可能会出现四种特殊情况：退化的解； 无界的解； 可选择的最优解； 不存在可行解。

单纯形法

simplex method