割圆术

042 割圆术

魏晋时期刘徽所创立的运用极限思想证明圆面积公式和计算圆周率的方法。所谓割圆，即指圆内接正多边形边数倍增的过程。刘徽认为：圆内接正多边形的面积小于圆面积。若将圆内接正多边形边数逐次倍增，则其面积逐渐增大。“割之弥细，所失弥少。割之又割；以至于不可割，则与圆合体而无所失矣。”割圆术的基本想法是： 运用勾股定理由圆内接正n边形的面积可求得圆内接正2n边形面积，且圆面积S满足不等式：

S_2n2n+ (S_2n-S_n)

即圆面积是两个多边形面积序列的共同极限。刘徽运用其割圆术证明了《九章算术》所载的圆面积公式：“半周乘半径得积步 (圆面积)”，并推算出100π介于314(64/625)与314(169/625)之间。从而得到π≈3.14。后人称之为“徽率”。刘徽的割圆术为圆周率的研究奠定了理论基础，并提供了科学的方法。

割圆术Geyuanshu

对于一个已知圆，作它的一串内接（或外切）正多边形，随着边数的增加，这些正多边形的周长（边长之和）就会越来越接近圆周长，它们的面积就会越来越接近圆面积， 如果再建立一个绝对误差界限的公式， 就可以通过这种方法把圆周长(进一步地，圆周率)和圆面积计算到所需的任何精确度，这种计算方法就是割圆术。实际上，所作内接或外切图形可以是任何易于求得周长或面积的凸图形。
古埃及的阿默斯纸草书(约公元前1650，参见该条)第50题计算了一块圆形土地的面积，计算过程相当于取圆面积S≡ (8/9d)², 其中d为圆的直径。这相
当于取圆周率π= (16/9)23.1605。同书第48题实际上告诉人们这一结果是如何得到的。原题是：有一个边长为9的正方形，将其每边3等分，联结相邻的分点，得到一个八边形，试求其面积。解法是，首先求出这个正方形的面积是9²＝81, 从中减去角上四个三角形的面积共18，余数81—18=63就是这个八边形的面积。它同时可以被近似地看作该正方形内切圆的面积， 这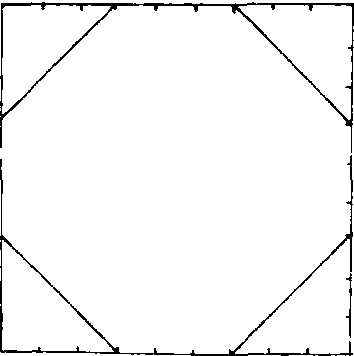
和边长为8的正方形的面积差不多， 由此立即得到第50题中的结果。结合这两个问题， 考虑到直到一千多年后中国、印度、希腊的圆周率值仍取为3, 而巴比伦
阿默斯纸常书中的圆面积计算最好的圆周率值不过是3.125，埃及人所得的结果是好得惊人的，而他们的方法体现了最早的用多边形面积近似圆面积的思想， 更是值得赞叹的。
历史上最早提出割圆术的是古希腊学者安提丰(Antiphon，公元前5世纪)，在研究化圆为方问题时，他想到用边数不断增多的圆内接正多边形的面积去近似圆面积。稍后的布莱松(Bryson)又用圆外切正多边形来做这一工作。在《圆的度量》中，阿基米德(公元前287——前212, 参见该条) 用割圆术证明了：
为了证明第3个结论， 阿基米德从圆内接与外切正六边形出发，逐步地把边数加倍，得到内接和外切正12、24、48和96边形，并计算它们的周长，结果求出了π的上界与下界。
在中国《九章算术》（参见该条）的方田章中给出了4条圆面积公式， 分别相当于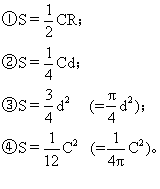
公元3世纪，刘徽（参见该条）为《九章算术》作注，独立地创造了割圆术。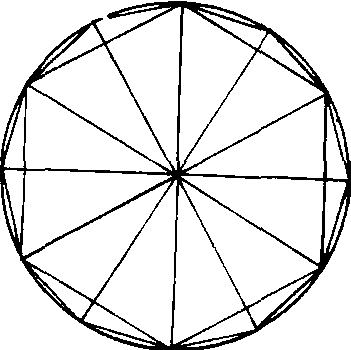
为了推求圆面积， 刘徽从圆内接正6边形开始计算， 它的边长等于圆的半径， 周长和面积都容易求得。为了叙述简便，我们记圆内接正n边形为pn，其边长为a_n, 面积为Sn。将正6边形p₆每边所对
的弧2等分，作出p₁₂，它的面积等于以圆半径R和a₆为对角线的6个筝形面积之和，而筝形面积等于对角线乘积的一半， 于是可求得S₁₂，利用勾股定理可以求得a₁₂。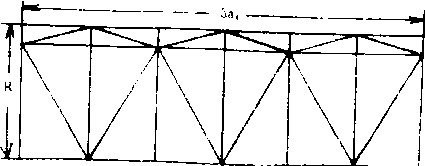

根据同样的步骤， 可以依次作出P24、P48、P96、……， 并可同样求得相应的面积和边长， 其周长是边数与

边长的乘积。
在求得S₁₉₂之后， 刘徽证明，
S₁₉₂192+ (S₁₉₂-S₉₆) (*)
由此及S_96、S₁₉₂的值估得圆面积S的值， 相当于得到
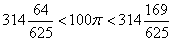
弃去在分数部分，得到100π=314，即π=3.14。仿照上述过程，刘徽由P3072求得π=3.1416。如果将 (*)
式一般化， 可得到一个十分有用的不等式：

S₂n 2n + (S₂n-Sn)

(* *)
n=3, 4, 5, ……
当n无限增大时，S_2n-S_n的值趋向于0，而S_n的值(S_2n
刘徽虽然没有明确概括出(* *)式，但他正是基于这一思想证明圆面积公式的， 这是极限思想在中国古代数学中的光辉体现。
公元5世纪， 祖冲之求得3. 1415926<π<3. 1415927，所用方法不详。
利用割圆术， 1427年，阿拉伯数学家阿尔 ·卡西(al-kashi) 得到π的16位小数值； 德国数学家柯伦(即鲁道夫，Ceulen, Ludolph van, 1540—1610)尽其一生将π值求到35位小数； 1630年， 格林伯根(Grienbergen)求至39位小数， 这是历史上用割圆术求π值的最高纪录。
另一方面， 由割圆术中体现出来的用多边形逼近曲边形的思想给人以深刻的启发， 它在公元前4世纪导致希腊人创立了穷竭法， 是数学史上向微积分迈进的重要一步。

割圆术

中国古代计算圆周率和圆面积的方法。刘徽根据圆内接正多边形的边数逐步增加时，其周长逼近圆周长，面积逼近圆面积，在所注《九章算术》中提出此法。