判别分析panbie fenxi

判别一个多指标样品属于何个多元总体的统计方法。如有K类不同数学能力水平的被试者， 每类被试者均可用统一的p个测验成绩描述，称作存在k个p元总体G₁, G₂，……，G_k。若从各类被试中分别随机抽取一组被试者进行观测， 共得k个样本，每一样本均是n_i(第i类的被试者数)个p维成绩向量， 于是就可按一定的最优准则建立一个相应的判别规则。以后，任一被试者的p维成绩向量：

就可按判别规则决定该属何个总体，即决定y∈G_i,i=1，或2, …，或k。由不同的最优准则可建立不同的判别规则。按不同的最优准则或判别规则分， 有距离判别、贝叶斯判别、费歇判别三种。在判别分析中，各总体G_i, i=1, 2, ……，k之间必须具有显著差异，故须进行总体均数向量的差异显著性检验和讨论误判概率的大小。

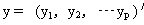
判别分析discrimenatory analysis

是判别个体所属类别的一种多元分析统计方法。如根据病人的各种症状判别病人患的是哪一种疾病，根据细菌的形态及生化特性判别属于哪一菌种，根据心电图各种波形特点识别心脏病等。因判别准则不同，又分为Fisher与Bayes等判别分析法。

判别分析

判别分析是判别个体所属类别的一种多元统计分析方法。它在医学上有着广泛的应用。例如，根据病人的各种症状判别病人患的是哪一种疾病； 根据病人各种症状的严重程度预测病人的预后； 根据细菌的形态及生化特性判别属于哪一菌种等。如果所用指标是某种图象的各种特征，则可将此法用于图象识别。例如，根据骨瘤X线片上的各种特征判别骨瘤性质； 根据心电图各种波形特点识别心脏病等。当应用电子计算机来进行分析时，就成为电子计算机辅助诊断，心电图自动识别等等。在判别分析中，因判别准则的不同，又有Fisher与Bayes等不同判别分析法。
判别分析的步骤可用诊断疾病为例说明如下：
(1)收集一批已确诊病人（或健康人与病人）的各种特征(可用于诊断的症状、体征、化验结果以及年龄、性别等)的资料，以m种特征为自变量(X₁,X₂，…X_m)，以诊断结果为应变量(Y)。
(2) 按照某一判别准则，求得一个或几个线性判别式（判别函数）。
(3)将新病人的各种特征值（检查结果）代入判别式，根据计算所得的Y值即可判断病人患何种疾病。
由以上步骤可知，判别分析的目的就是要根据已知类别(如有G类)的一批样本找出一个将这G类事物区分开来的方法。
Fisher判别法 Fisher判别的直观意义是如果两种疾病的某些症状（指标）很相似，则仅凭某一症状往往不能区分这两种疾病，因为两种疾病的这一症状的观察值会有很大程度的重叠；但若将几个症状综合起来，用数学方法找出这些症状的一个适当的线性组合，那么就可使重叠程度大大减少，从而就能比较正确地、可靠地分辨这两种疾病。这个线性组合可以作为一种综合指标，用以区分两类事物。如果对于两种疾病A与B，考虑只有两个变量（指标）X₁与X₂的情形，则两指标的线性组合
Y=b₁X₁+b₂X₂ (1)
可作几何解释如下： 图1说明仅凭一个指标X₁或X₂时，A、B两病的每一指标的观察值都会有很大程度的重叠；但如以X₁为横坐标，X₂为纵坐标，并设法在此X₁X₂平面内找到这样一个Y轴，使X₁X₂平面上的散点投影到Y轴上时，两种疾病观察值的重叠小于任何其他轴，如图所示，则综合指标Y区别A、B两种疾病的能力显然将大于X₁或X₂。

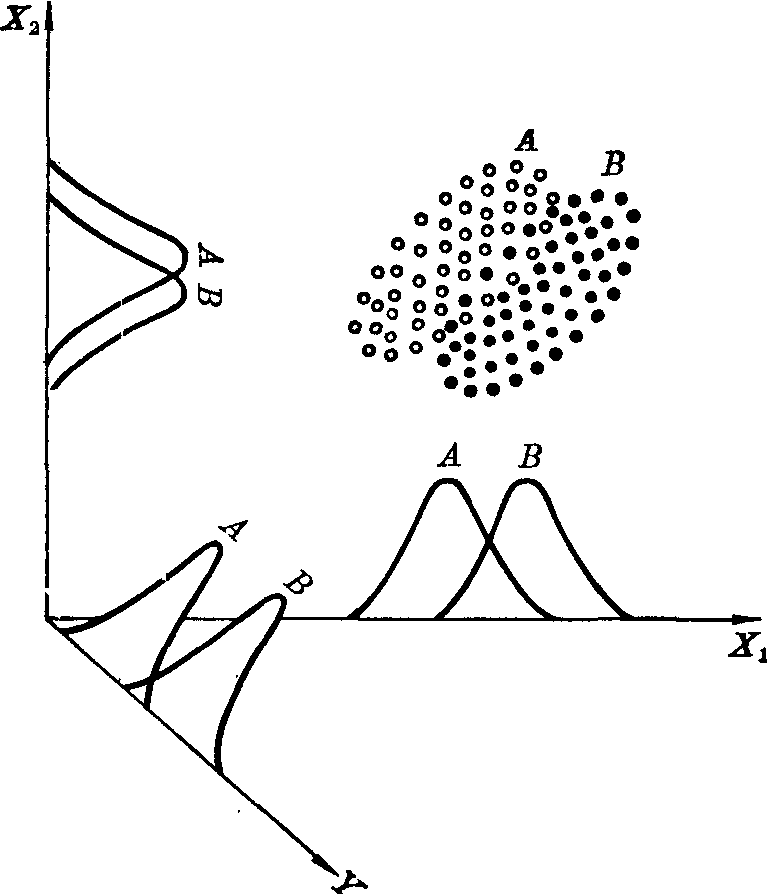
图1 两个指标综合示意（判别分析的几何解释）

式(1)称为判别函数。如果指标不是两个而有m个，则判别函数为

Y=b₁X₁+b₂X₂+…+b_mX_m。(2)

有了判别函数就能有效地判别两类个体的归属。有时一个判别函数不能有效地判别多类个体，这时就需要用几个判别函数。
Fisher判别准则是要求各类之间的变异尽可能地大，而各类内部的变异尽可能地小，变异用离均差平方和表示。以两类判别为例，即要求：

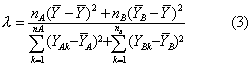
为最大，式中n_A与n_B分别为A类与B类的例数，Y_Ak与Y_Bk分别为A类与B类中第k例的Y值，A与B分别为A类与B类的均数，为两类合并后的总均数。根据这一准则，式(2)中的系数b_i可由下列方程组解得：

式中l_ij为各指标各类内部的离均差平方和或积和。在两类判别时，

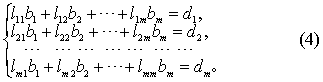
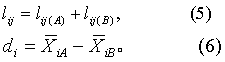
求得b_i后，代入式(2)即得判别函数。
求判别界值Y₀:把A类、B类的各指标的均数分别代入式(2)得：

然后以两均数之中点作为两类的界点。

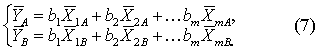
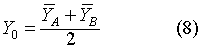
判别效果的检验：若判别函数能划分两类总体，则两类总体的均数不等；反之，则两总体均数相等。
设样本来自协方差矩阵相同的两个多元正态总体，则两类总体均数有无差异可用F检验：

自由度v₁＝m,v₂＝n_A+n_B-m-1。式中D2为Maha-lanobis距离。

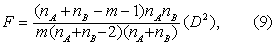
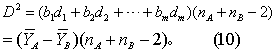
求得F值后，查F界值表得P值，按所取检验水准作出推断结论。当拒绝H0，接受H1，则认为变量的判别效果有显著性，即建立的判别函数有效。
例1 拟研究以舒张期血压和血浆胆固醇含量预测病人是否患冠心病，测定15名冠心病人和16名健康人的舒张压X1及血浆胆固醇含量X₂，结果见表1，试作判别分析。

表1 冠心病人与健康人舒张压(mmHg)和血浆胆固醇含量(mg/dl)^*

冠心病组(A类)			正 常 组(B类)
编号(Ak)	X1A	X2A	编号(Bk)	X1B	X2B
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	74 100 110 70 96 80 80 100 100 100 90 110 100 96 100	200 144 150 274 212 158 172 140 230 220 239 155 155 140 230	1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16	80 94 100 70 80 80 70 80 80 80 78 70 80 80 84 70	80 172 118 152 172 190 142 107 124 194 152 190 104 94 132 140
	1406	2819		1276	2263

*为便于理解，本例数据经过修改。
(1)求判别函数。计算各类的基本数据及离均差平方和、离均差积和：

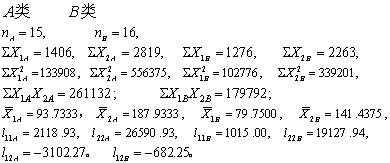
按式(5)计算各指标两类内部的离均差平方和或积和的合并值：
l₁₁ =2118.93+1015 =3133.93,
l₂₂ = 26590.93+19127.94 =45718.87,
l₁₂＝l₂₁ =-3102.27+(-682.25)=-3784.52。
按式(6)计算各指标两类均数之差：
d₁＝93.7333-79.7500=13.9833,
d₂＝187.9333-141.4375=46.4958。
将上列结果代入式(4)得

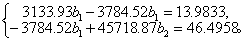
解之得 b₁ = 0.006321,
b₂＝0.001539。
代入式(2)得判别函数为：
Y=0.006321X1+0.001539X₂。
按式(7)与(8)求两类的判别界值Y₀:

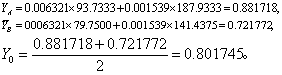
(2)检验判别函数的有效性。
H₀: μA=μB,
H₁: μA≠μB。
a=0.01。
按式(10)及式(9)得：

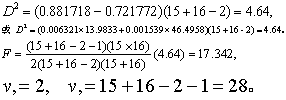
查F界值表得P<0.01，按a=0.01水准拒绝H₀，接受H₁，故可认为判别函数有效。
(3) 回代。如以A类的第1例X₁＝74,X₂＝200代入判别函数，得Y=0.775554Y₀，判断为冠心病人，此例判对了。仿此将每例都进行判断，结果见表2。
由表2可见两类错判的各有3例，判对的共25例，故符合率为25/31=80.64%。

表2 判别分析与临床诊断结果符合情况

临床诊断	判别结果		合计
	冠心病类	正常人类
冠心病类 正常人类	12 3	3 13	15 16
合 计	15	16	31

用双指标(X₁ 、X₂)作两类判别的判别图根据(X₁、X₂)描点于X₁X₂坐标平面，并在此平面上画出判别轴：
b₁X₁+b₂X₂＝Y₀,(11)
此轴将平面划分为A、B两个区域。于是根据观察对象所测得数据(X₁,X₂)标在图上，根据点子所落入的区域即可判别此对象所属的类别。如图2。
例2 根据例1的结果（经检验判别函数有效），试作判别图，并对某受试者：X₁＝90mmHg,X₂＝165mg/dl，判断其归属。
(1)作判别图。以X1为横坐标，X2为纵坐标，并以0.006321X₁+0.001539X₂＝0.801745为判别轴，作成图2的判别图。
将表1的数据依次描点，回代结果可看出A、B两类错判的各有3例，其余均符合，同表2。

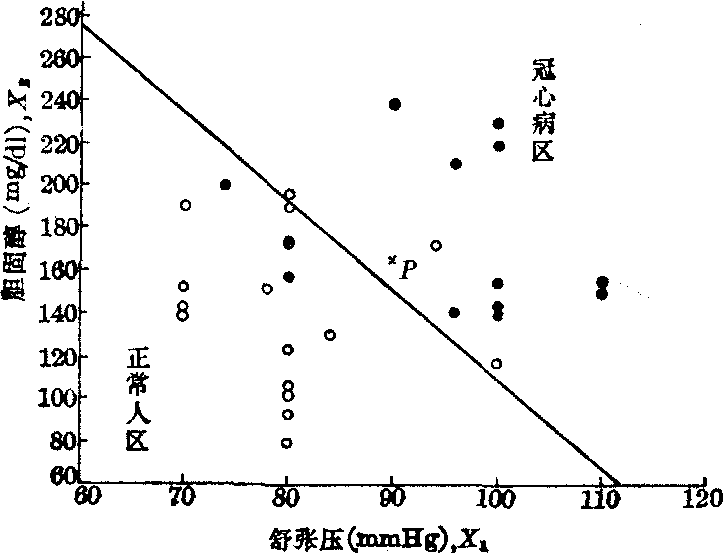
图2 判别分析图示法

(2)判别归属。以受试者的观察值(90,165)，描点P于判别图，由于点P落入冠心病区，故判断受试者患有冠心病。另一判别法是以X1=90,X2=165代入判别函数，得Y=0.006321 × 90+0.001539×165=0.822825。
例1已算得：A=0.881718,B= 0.721772, Y₀＝0.801745，则本例B0<A。 今Y₀Bayes判别法 Bayes判别准则是以个体归属某类的概率（或某类的判别函数值）最大或错分总平均损失最小为标准。
设有某个体来自G个不同总体之一。我们用L(h|g)表示把实属总体g类的个体错分入总体h类的“错分损失”，相应的错分概率记为P(h|g)，则把实属g类的个体错分入他类的“错分平均损失”为
各类互相错分的总平均损失为

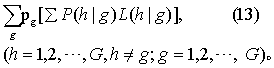
式中pg为个体来自总体g类的可能性（即先验概率）。设各类总体都服从多元正态分布，并且各类总体的协方差矩阵相同，错分损失L(h|g)=1(g≠h)，则由式(13)可推导得G类中每类的判别函数为

对于任一观察对象甲，只要把实际测得的各指标Xj值代入式(14)即可求得各类的Y值，哪个Y值最大，就判断甲属于该类。若式(14)中的先验概率相等时，则式中的ln pg可全部删去而不影响判断结果。 若pg不知时，可由各类的频率估计之。
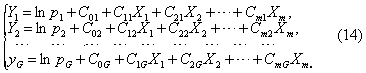
例如某单位研究乳房肿块的计算机鉴别诊断，收集了183例的体检和病史资料，根据5个指标(年龄X₁，肿块距乳头距离X₁₅，肿块宽度X₁₈，活动度X₂₁及对侧有无肿块X₂₆)作三类判别。按Bayes准则建立判别函数后，进行回代结果如表3，回代符合率为(23+73+45)/183=77.05%，可见效果不太理想。后又以11个指标作两类判别取得了良好效果，回代符合率达96.72%，见表4。

表3 五个指标三类判别效果

计算机诊断	病 理 诊 断			合 计
	癌	纤维腺瘤	乳腺病
癌 纤维腺瘤 乳腺病	23 5 1	3 73 13	1 19 45	27 97 59
合 计	29	89	65	183

表4 11个指标二类判别效果

计算机诊断	病 理 诊 断		合 计
	癌	良性肿块
癌 良性肿块	27 2	4 150	31 152
合 计	29	154	183

判别分析的其他方法 判别分析种类很多，也有非参数的判别分析法。判别分析法过去用于连续变量的较多，如果要用于定性资料，则要用到数量化理论。目前离散变量的判别方法也有很大发展。用Bayes逆概率公式和极大似然法也可以判别个体属于哪一类。有人也把它们归入判别分析。
逐步判别是用类似逐步回归的方法对指标先进行筛选。方法有多种，其中最常用而较简便的是S.S. Wilks所提出的方法，在选出变量后再作判别分析。上述乳房肿块的计量诊断中所用的5个和11个变量就是按Wilks统计量用F检验筛选出来的。
序贯判别是在二类判别时先用一个指标作判别，判别结果可以是“A类”、“B类”或“不定”。当判为“不定”时再用第二个指标进行判别，如此序贯地逐一引入指标作判别。

判别分析discriminant analysis

这是多元分析中的主要方法之一。其一般表述为：设有M个总体G₁,G₂，…，G_m，它们具有相同的p个可观测指标X_i,i=1,2，…，p。对于不同的G_i,i = 1,2，…，m，这些指标有不同的统计特性。现假定有一个样本X⁽⁰⁾＝(X₁⁽⁰⁾,X₂₍₀₎，…，X_p⁽⁰⁾)来自这M个总体中，但不清楚其到底来自哪个总体。判别分析就是要通过相关统计知识和经验，去判断该样本究竟来自哪一个总体。解决这个问题的途径很多。常用的判别方法有贝叶斯(Bayes)判别、距离判别、费希尔(Fisher)判别和线性判别等等。对于在实际判断中可能出现的误判情况，解决方法就是要在判别分析中选取一种准则。如选取误判概率或损失，使得误判的概率或误判的损失尽可能小。
判别分析在实际中的应用很广。在研究经济问题中，常用于经济现象的多指标分析。例如，可根据历史资料，选择如国民生产总值、工业总产值、人均消费水平等多项经济指标，判别一个国家或地区的经济发展状况。

判别分析discriminant analysis

用于判别样品所属类型的多元分析方法。基本原理是按照一定判别准则，建立一个或多个判别函数，用研究对象的大量资料确定判别函数中的待定系数，并计算判别指标，据此确定某一样品属于的类别。判别问题的提法为： 设有k个已知总体，从各个总体中分别抽取一个样本。另有一个样品，它属于且只属于其中的一个总体。要判别它属于哪个总体。根据对判别问题的不同解释，有三种不同的常用的判别方法： 距离判别、贝叶斯判别和费希尔判别。

判别分析

多元分析的一种。主要用于判别样品所属类型。判别问题的提法为： 设有k个已知总体，从各个总体中分别抽取一个样本。另有一个样品，它属于且只属于其中的一个总体。现在要判别它属于哪个总体。根据对判别问题的不同解释，有三种不同的常用的判别方法，距离判别、贝叶斯判别和费希尔判别。