全概率公式quangailu gongshi

在给定的随机试验中，事件A的发生往往与事件B₁ ,B₂ ,B₃ ，………的发生有关，B₁,B₂,B₃，………称为原因，A称为结果，各种原因对结果的影响是不同的，或者说，发生结果的可能性与各种原因发生的可能性有关。为表达这种关系，可应用下述全概率公式：
若对于事件组B₁,B₂，………，满足：
❶ B_iB_j＝Φ (i≠_j);;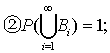
❸P (B_i)>0 (i=1,2，………)，则对于任意一事件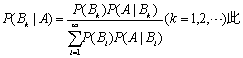有

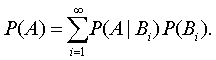
若B_i只有n个，公式也成立。此时右端只有n项相加。
比如，有三个形状相同的口袋，在第一个口袋中装有2个红球和1个白球，在第二个口袋中有3个红球和1个白球，在第三个口袋中有2个红球和2个白球。若某人任取一个口袋，从中任取一球，求取得红球的概率。
用A表示 “取得红球”事件，用B_i表示 “取自第i口袋的球”(i=1,2,3)。于是A=AB₁∪AB₂∪AB₃。由全概率公式知
P (A) =P (AB₁) +P (AB₂) +P (AB₃ ) =P (B₁) ×P (A| B₁) +P (B₂ ) P (A|B₂) +P (B₃ ) P (A| B₃)
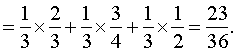
利用全概率公式，可将确定事件A的概率分解为确定事件AB₁,AB₂，………，AB_n的概率。

全概率公式formula of total probability

由已知的简单事件的概率求解复杂事件的概率的数学方法。概率论中，求复杂事件概率时，往往把它分解成若干个互不相容的简单事件，然后依据条件概率和乘法公式，求出简单事件的概率，最后根据概率可加性得到复杂事件的概率。具体为： 设实验E的样本空间为S,A为E的事件，B₁,B₂, …，B_n为S的一个划分，且P(B_i)>0(i=1,2, …，n)，则 P(A)=P(A|B₁)×P(B₁) + P(A|B₂)×P(B₂) +… + P(A|B_n)×P(B_n)，此式即全概率公式。