假设检验jiashe jianyan

见统计推断。

假设检验

为了解总体某些统计性质（如总体某个数字特征或总体是否服从某一分布等），或多个总体某些性质进行比较，常采用一种称之为假设检验的方法。其做法是：首先根据需要作出的判断，提出一个假设，然后利用从总体中抽取的样本所提供的资料，用一定的方法检验假设的合理性，最后对假设的合理性作出判断。假设检验分为参数检验和非参数检验两大类。假设检验的步骤一般按如下步骤进行：第一，拟出欲检验的零假设H₀（即写出要检验的假设的具体内容）和拟出备择假设H₁；第二，选取适当的检验统计量，并根据样本计算出该检验统计量的观测值；第三，依照给定的显著性水平，查检验统计量所服从的分布的临界点数值表，确定临界点和拒绝域（或接受域）；第四，作出判断，如果检验统计量的值落入拒绝域就拒绝零假设H₀，如果检验统计量的值落入接受域，就没有理由拒绝零假设H₀，也就意味着接受了零假设H₀。这种检验常被应用于测验分数统计中。

假设检验

数理统计的一个重要内容。通常对总体的概率分布或其中的参数作假设，然后通过计算样本值在一定可靠程度上作判断——接受或拒绝原假设。

假设检验Test of Statistical Significance

亦称“显著性检验”。用来判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。其基本原理是先对总体的特征作出某种假设，然后通过抽样研究的统计推理，对此假设应该被拒绝还是接受作出推断。具体做法是：根据问题的需要对所研究的总体作某种假设，记作H₀；选取合适的统计量，使得在假设H₀成立时，其分布为已知；由实测的样本，计算出统计量的值，并根据预先给定的显著性水平进行检验，作出拒绝或接受假设H₀的判断。常用的假设检验方法有U检验法、T检验法、F检验法等。

假设检验

假设检验和参数估计是统计推断的两个重要领域。假设检验就是先对总体的参数或分布作出某种假设，如假设总体均数（或总体率）为一定值，两个总体均数（或总体率）相等，总体服从正态分布或两总体分布相同等； 然后用适当的方法根据样本对总体提供的信息，推断此假设应当拒绝或不拒绝。其结果将有助于研究者作出决策，采取措施。假设检验有参数法与非参数法，其意义见条目“非参数统计”。
显著性检验常作为假设检验的同义语。显著性检验一词历史上沿用已久，目前仍较普遍应用。显著性检验的思想至少可追溯到十八世纪，但至本世纪才以决策论的思想明确提出检验假设和备择假设，并引入第一类错误和第二类错误的概念，形成了系统的假设检验理论。
假设检验的一般步骤如下：
(1) 建立假设： 先要明确分析的目的要求。不同类型的资料，往往分析的指标也不同，如计量资料常作均数间的比较，计数资料常作率或构成比间的比较。又如两样本均数作比较时，若要求推断两组总体均数有无差别，这就包括甲组均数高于乙组和乙组均数高于甲组两种不同的情况，应该用双侧检验；若仅要求推断甲组均数是否高于乙组（比如从专业知识已知甲组均数不会低于乙组），就应该用单侧检验；同样，若仅要求推断甲组均数是否低于乙组（比如从专业知识已知甲组均数不会高于乙组），也应该用单侧检验。双侧检验比单侧检验常用，特别是对预初试验结果的考虑，思路宽些比窄些为好。
假设有两种： 一种是检验假设，符号为H₀; 一种是备择假设，符号为H1。二者都是根据统计推断目的而提出的对参数或分布特征的假设。H0是从反证法的思想提出的，H₁是和H₀相联系的、对立的假设。例如，为了检验两总体均数是否相等，通常H₀为两总体均数相等，即两种处理的效果无差别；H₁为两总体均数不等，即两种处理的效果有差别。现以常用的样本均数的比较为例，用符号表示如下。
样本均数(其总体均数为μ)与某已知总体均数μ0作比较：

	目 的	H0	H1
双侧检验 单侧检验	是否μ≠μ0 是否μ>μ0 或是否μ<μ0	μ=μ0 μ=μ0 μ=μ0	μ≠μ0 μ>μ0 μ<μ0

两样本均数(其总体均数分别为μ₁与μ2)作比较：

	目 的	H0	H1
双侧检验 单侧检验	是否 μ1≠μ2 是否 μ1>μ2 或是否 μ1<μ2	μ1=μ2 μ1=μ2 μ1=μ2	μ1≠μ2 μ1>μ2 μ1<μ2

(2) 确定检验水准： 亦称显著性水准，符号为α。α是假设检验发生第一类错误的概率。它是结合具体问题，联系第二类错误的概率确定的（详后）。以t检验为例，单侧检验时，α指t分布曲线下一侧尾部的面积 [图1(a)]；双侧检验时，α指t分布曲线下两侧尾部面积的和[图1(b)]。通常取α=0.05或α=0.01。由图1可见，当α确定后，则横轴上的对应界值tα也就确定了。

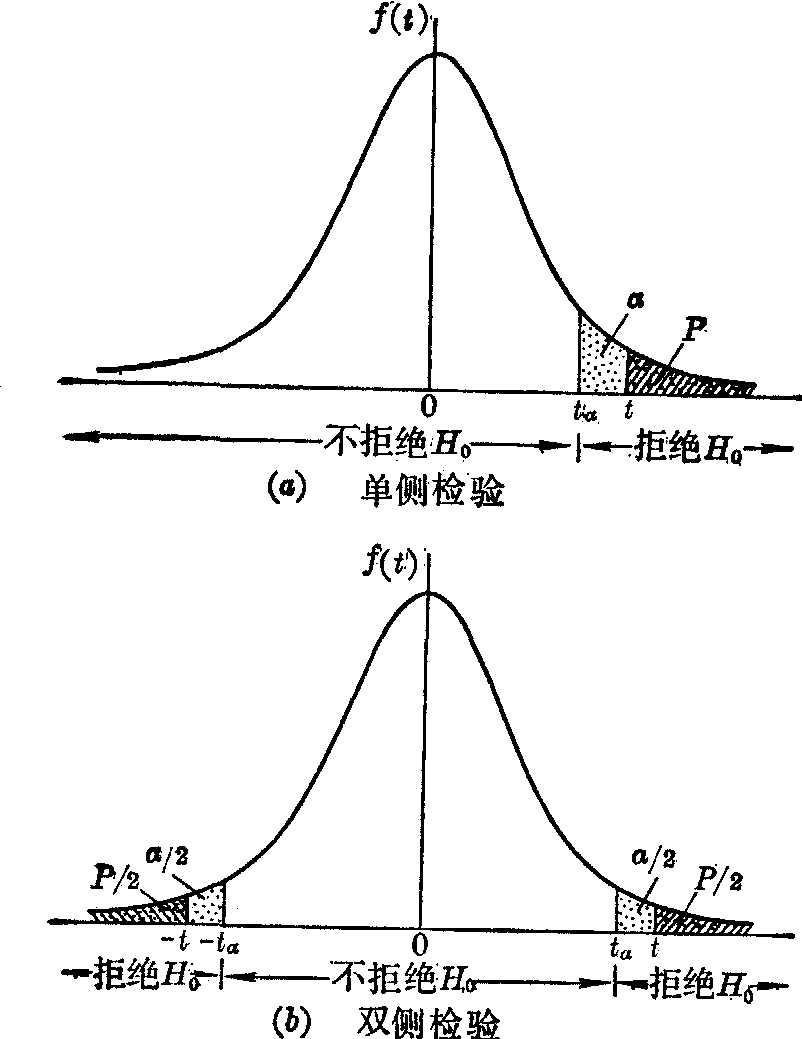
图1 假设检验示意(以t检验为例)

(3) 选定检验方法和计算统计量的观察值： 根据研究设计的类型和统计推断的目的要求选用不同的检验方法。如完全随机设计中，两样本均数的比较常用t检验，多个样本均数的比较常用F检验，两个或多个样本率的比较常用x²检验等。
统计量属样本指标，是样本数据的函数。不同的检验方法要用不同的公式计算现有样本统计量的观察值，如t检验要用特定的公式计算t值，x²检验要用特定的公式计算x²值。不同的统计量通常有其特定的抽样分布，如图1的t分布。
(4) 求P值： P值是指由H₀所规定的总体作随机抽样，获得等于或大于统计量观察值的概率。如图1，单侧检验时，P值是指横轴上等于或大于统计量观察值（取绝对值） t时，曲线下一侧尾部的面积；双侧检验时，P值是指横轴上等于或大于统计量观察值（取绝对值） t时，曲线下两侧尾部面积的和。求P值的方法一般有两种：
❶直接计算，如四格表的确切概率法；
❷查统计量分布的分位数表（简称界值表）求得，此法最常用。如下表摘录了自由度v=20时t的界值，符号为tα,v。表中P(1) 为

t界值表（摘录）

v	P(1): 0.25	0.10	0.05	0.025	0.01	0.005
	P(2): 0.50	0.20	0.10	0.05	0.02	0.01
20	0.687	1.325	1.725	2.086	2.528	2.845

单侧检验的概率，P(2)为双侧检验的概率。如单侧检验t_0.05,20＝1.725，它的意思是当v=20时，按统计量t的分布规律，理论上有5%的|t|值等于及大于1.725，或者说抽得统计量|t|等于及大于1.725的概率为0.05；同理，双侧t_0.05,20＝2.086，意思是说，当v=20时，抽得统计量|t|等于及大于2.086的概率为0.05。显然，双侧检验时，若算得统计量观察值|t|>2.086，则P<0.05；若|t|<2.086，则P>0.05，余类推。因而P值易由表直接查出。如双侧检验，v=20时，算得统计量观察值t=2.425，在界值2.086与2.528之间，则0.05>P>0.02；若t=2.086，则P=0.05; 若t=0.535，则P>0.5，余类推。由表及图1可见，自由度相同时，双侧t2α等于单侧tα，因为t分布是中心为0的对称分布。
(5) 作出推断结论： 当P≤α时，结论为按所取检验水准拒绝H0，接受H1；当P>α时，结论为按所取检验水准不拒绝H0，或者说接受H0。如H0为μ1 =μ2,H1为μ₁≠μ2，拒绝H₀，可认为两总体均数有差别；不拒绝H₀，则尚不能认为两总体均数有差别，必要时可继续研究。这样作出结论的理由是：在H0成立的条件下，出现等于及大于统计量观察值（常取绝对值）的概率很小，P≤α，即现有样本信息不支持H₀，因而拒绝它；相反，如P>α，即现有样本信息支持H0，就没有理由拒绝它，有时只好接受它。须知： 拒绝H0，不能认为H0肯定不成立，因为在H0成立的条件下，出现现有样本的概率虽小，但仍有可能出现，只是可能性很小而已；同理，不拒绝H0，也不能认为H0肯定成立。因为假设检验时，通过样本观察，必须对被检验的假设作出明确的判断，只能从“拒绝”或“不拒绝”中选择一个较为合理的决定。由此可见，统计推断的结论是具有概率性质的，不管是拒绝H0或不拒绝H0，都有可能发生错误，即第一类错误或第二类错误，但可以指出发生错误的概率有多大。
进行假设检验时应注意：
❶资料来源必须遵循严密的随机抽样设计。
❷选用检验方法应符合其适用条件。
❸结论中拒绝H₀，接受H₁，习惯上亦称“显著”，不应误解为相差很大，或在医学上有显著的实用价值；反之，不拒绝H₀，习惯亦称“不显著”，不应误解为相差不大，或肯定无差别。例如两样本均数作比较时，拒绝H₀:μ₁＝μ2，接受H₁:μ₁≠μ2，不应误解为μ₁与μ₂的差别很大；不拒绝H0，不应误解为μ1与μ2相差不大或一定相等。习惯上将H0称为无效假设。为不致误解，有的统计学家主张不用“显著”、“无效”等词。
❹结论不能绝对化。因为检验水准是根据分析要求确定的，实际工作中，对同一问题要求α的大小往往有一定的灵活性，有时按α=0.05水准拒绝H₀，而按α=0.01水准有可能不拒绝H₀；再者，取同一检验水准，就现有样本不拒绝H₀，但增加样本含量，由于减少抽样误差，有可能拒绝H0。因此，P接近α时，下结论要慎重。此外，拒绝H0可产生第一类错误，不拒绝H0可产生第二类错误。
❺报告结论时，应列出统计量的观察值，注明采用的是单侧检验或双侧检验及检验水准，并写出P值的确切范围，如0.05>P>0.02，以便读者按自选的检验水准作出结论。
第一类错误和第二类错误 由假设检验作出的推断结论可能发生两种错误：
❶拒绝了实际上是成立的H₀，这叫第一类错误或Ⅰ型错误。如图2，设H0: μ=0,H1:

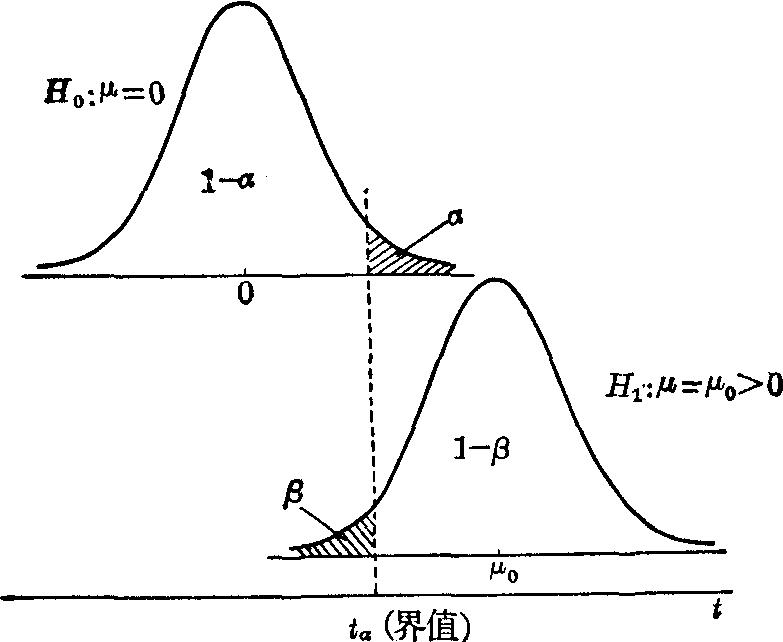
图2 第一类错误与第二类错误示意(以单侧t检验为例)

μ>0。若μ确实为0，则H0。实际上是成立的，但由于抽样的偶然性，得到了较大的t值，因 |t|≥tα,P≤α，按所取检验水准α拒绝H₀，接受H₁，结论为μ>0，此推断当然是错误的。
❷不拒绝实际上是不成立的H0，这叫第二类错误或Ⅱ型错误。如图2，设H0: μ=0,H1: μ>0。若μ确实大于0，则H 0实际上是不成立的，但由于抽样的偶然性，得到了较小的t值，因 |t|α，按所取检验水准α接受H0，而未拒绝μ=0的错误假设，此推断当然也是错误的。
第一类错误的概率用α表示，假设检验时，根据分析者的要求确定其大小，如确定α=0.05，即第一类错误的概率为0.05，理论上100次抽样中发生这样的错误有5次；第二类错误的概率用β表示，它只有与特定的H₁结合起来才有意义，但β值的大小很难确切估计，仅知样本含量确定时，α愈小，β愈大；反之α愈大，β愈小。如图2，移动界值tα，此理易明。图2中的1-β称为检验效能或把握度，即两总体确有差别，按α水准能发现它有相差的能力。例如1-β=0.90，若两总体确有差别，则理论上在100次抽样中，有90次能得出有差别的结论。总结如下：

客观实际	拒绝H0	不拒绝H0
H0成立 H0不成立	第一类错误(α) 推断正确(1-β)	推断正确(1-α) 第二类错误(β)

α和β可以根据分析要求适当控制。要同时减少α及β，唯一的方法是增加样本含量；当样本含量确定后，虽然不能同时减少α和β，但可以通过确定α值来控制β。若要求重点在减少α，一般取α=0.01；若重点在减少β，一般取α=0.05，因为β虽属未知，但估计比取α=0.01时小些。当然α亦可取其他水准，须视具体问题的容许大小而定，不宜千篇一律。

假设检验

见“统计检验”条。

假设检验test of hypothesis

根据随机变量总体x的样本对关于x分布的一个统计假设做出接受或拒绝的判断的一类统计推断。设x的分布函数F(x;θ)的函数形式已知，而θ为未知参数，θ的取值范围Θ为参数空间，根据对x作的n次观察值x₁,x₂，…，x_n，对关于θ的一个陈述句“θ∈Θ₀”((H)是Θ的一个子集)做出接受或拒绝的判断问题，即为参数假设检验。称待检验的陈述句H₀:“θ∈(H)”为拟定假设（或原假设），与H₀相反的陈述句H₁:“θ∈Θ-Θ₀”，称为对立假设（或备择假设）。假设检验也可能是关于分布的假设检验问题，如F(x;θ)的函数形式未知，需要判断是否和某一已知分布函数F₀(x)一样，或需要判断两个分布函数F₁(x)、F₂(x)是否相同等。
对拟定假设H₀做出接受或拒绝的判断，应先确定样本空间到只包含两个元素的集合{拒绝，接受}上的一个对应规则，在这个对应下，如果样本空间中的点(x₁′，…，x_n′)对应着“拒绝”，则当得到样本(x₁″，…，x_n′)时就拒绝H₀，只要将对应于“拒绝”的点明确了，就确定了一个对应规则，即一个检验方法，因为不对应“拒绝”，就意味着对应“接受”。一切对应于“拒绝”的点组成样本空间的一个区域S，称之为拒绝区域(或临界区域、判别区域)。
样本点x是否落入拒绝区域S是有一定的概率的。有时即使拟定假设H₀实际上正确，而x却落入S而导致拒绝H₀，这就犯了一种错误，犯了“弃真”错误，常称为第Ⅰ型错误，犯这种错误的概率常记作α，即P{拒绝H₀|H₀为真}=α,α称为显著性水平。自然希望将α取得比较小，如取α为0.05、0.01等，α取定后即可确定拒绝区域S。当H₀不正确时，也可能由于xS而导致接受H₀，这也是一种错误，即所谓“存伪”错误，常称为第Ⅱ型错误，犯这种错误的概率常记作β。当然，也希望β较小，但实际上，在一定的样本容量条件下，要同时减小α和β是不可能的，减小其中一个，另一个就会增大。
假设检验问题中拟定假设H₀:θ∈Θ₀,Θ₀只含一个点，或对立假设H₁:θ∈Θ-Θ₀,Θ-Θ₀中也只含一个点时，称只含一个点的假设为简单假设，否则即为复合假设。从拒绝域的设置情况看，如总体均值μ的检验中，H₀:μ=μ₀;H₁:μ≠μ₀的假设检验为双边检验；H₀:μ=μ₀;H₁:μ>μ₀(或H₁:μ<μ₀)的假设检验为单边检验。从临界区域看，在α固定不变的各临界域中，能使β为最小的，称为最佳临界域。又若对立假设为复合假设，β小于α时，则依此所定的临界域为无偏临界域。若临界域满足无偏、又满足最佳条件，即为最佳无偏临界域。

假设检验test of hypothesis

根据样本的信息判断总体是否具有指定特征的一种方法，通常是根据问题的性质和研究的需要建立假设，再按一定的方式来推断这种假设的可靠性。分为参数假设检验和非参数假设检验。前者检验某一总体指标是否等于某一数值；后者检验某一随机变量是否服从正态分布。

假设检验test of hypothesis

根据样本的信息来判断总体是否具有指定的特征的一种方法，即根据抽样结果在一定可靠程度上对原假设作接受或拒绝的检验。例如已知样本来自服从正态分布的总体，问是否有理由说明它来自期望值为u的正态总体？如果已知相互独立的两个样本分别来自两个正态总体，怎样判断这两个总体的期望值或方差是否相同。假设检验通常是根据问题的性质和研究的需要建立假设，然后按一定的方式，通过抽取样本来推断这种假设的可靠性。假设检验可分为参数假设检验和非参数假设检验。前者检验某一总体指标是否等于某一数值；后者检验某一随机变量是否服从正态分布。

假设检验hypothesis testing

亦称“显著性检验”。根据一定假设条件由样本推断总体的数理统计方法。用来判断样本与样本，样本与总体差异是由抽样误差引起还是本质差别造成。假设主要包括根据数据资料作出一总体参数是否等于某一数值或某一随机变量，是否服从某种概率分布等。具体步骤是： (1) 根据问题需要对研究总体作出某种假设，记作H₀;(2) 选取合适统计量，此统计量的选取须保证假设H₀成立时，其概率分布已知；(3) 根据实际获得的样本数据，计算统计量的值，然后根据预先设定的显著性水平进行检验；(4) 作出拒绝或接受假设H₀的判断。

假设检验

根据从总体中抽取的样本，对总体的命题作出接受或拒绝决策的统计方法。