二元一次不定方程eryuan yici buding fang cheng

参见“数学课外活动”部分中的“二元一次不定方程”.

---

二元一次不定方程eryuan yiei budingfangcherng

指含有两个未知数的方程ax+by=c，其中a,b,c，都是给定的整数，并且ab≠0.研究二元一次不定方程的整数解，要解决下述三个问题：
❶整数解的存在问题；
❷若有整数解，其解的个数问题；
❸求出全部整数解^.
解的存在问题：二元一次不定方程

ax+by=c (ab≠0)　(1)

有解的充分必要条件是(a,b)|c.
证 设方程(1)有整数解(x₀,y₀)，则ax₀+by₀＝c.由于(a,b)|a,(a,b)|b，故由上式得(a,b) |c.条件的必要性得证.又，设(a,b)|c，令c=c₁(a,b)，其中c₁是整数，则存在整数s,t，使as+bt=(a,b)(参见“最大公因数”)，于是

a(c₁s)+b(c₁t)=c₁(a,b)=c

故原方程有整数解x₀＝c₁s,y₀＝c₁t.条件的充分性得证.
解的个数：若方程

ax+by=c　(其中ab≠0)

有一个整数解(x₀,y₀)，则它有无穷多个整数解，并且它的一切解可以表成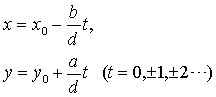

其中d=(a,b).
求出全部整数解的方法：由上述可知，为了求出全部整数解，只须先求出一个特解，进而归结为求出整数s,t，使得as+bt=(a,b)，求s,t的具体方法参见“最大公因数”.
例如，求252x-198y=36的全部整数解.因为(252,198)=18，而18|36，故原方程有整数解.把原方程约简为

14x-11y=2　(2)

先解14x+11y=1.用辗转相除法求出s=4,t=-5，使14s+11t=1.即14×4+11×(-5)=1.所以14×8-11×10= 2，即方程(2)的一个特解为x₀＝8,y₀＝10，故其所有整数解为

x=8+11t,y=10+14t(t=0,±1,±2，…).

这也是原方程的全部整数解.
必须指出，一次不定方程的一般解的表达式不是唯一的.例如，x₁＝19,y₁＝24，也是原方程的一个特解，这时一般解可以表成

x=19+11t,y=24+14t (t=0,±1,±2，…).

在实际问题中，有时需要求出二元一次不定方程的所有正整数解.其一般解法是，先求出这个方程的全部整数解的表达式，然后由此求出使x>0,y>0同时成立的整数解.