两直线的交点liangzhixian de jiaodian

已知直线A₁x+B₁y+C₁＝0和A₂x+B₂y+C₂＝0.❶当A₁B₂-A₂B₁≠0时，两直线相交，有唯一的公共点，坐标为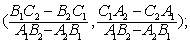

❷当

A1B2-A2B1＝0,

且

B₁C₂-B₂C₁≠0)(或C₁A₂-C₂A₁≠0)时，两直线平行.无公共点；
❸当A₁B₂-A₂B₁＝B₁C₂-B₂C₁＝C₁A₂-C₂A=0时，两直线重合，有无穷多个公共点.
利用行列式可简化上述结论的表述：设

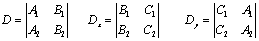
❶当D≠0时，两直线相交，有唯一公共点，坐标为(Dx/D,Dy/D);
❷当D=0，但Dx,Dy不全为零时，两直线平行，无公共点；
❸当D=Dz=Dy=0，两直线重合，有无穷多个公共点.
若A₂,B₂,C₂全不为零时，上述结论可简化为：
❶当A₁/A₂≠B₁/B₂时，两直线相交，有唯一的公共点，坐

标为

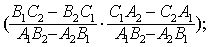
❷当

A1/A2＝B1/B2≠

C₁/C₂时，两直线平行，无公共点；
❸当A₁/A₂＝B₁/B₂＝C₁/C₂时，两直线重合，有无穷多个公共点.