不定积分的第二换元积分法
不定积分的第二换元积分法budingjifen de dierhuanyuan jifenfa
设函数x =φ(x)单调、可导,且ψ′(t)≠0,又设f[ψ(t)〕ψ′(t)具有原函数φ(t),则根据换元公式
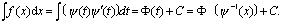
第二换元积分法的基本思路:若∫ f(x)dx不易求,可适当选择x = ψ(t),将原不定积分化为
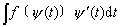 的形式;而
的形式;而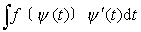 容易求出,且等于ψ(t) +C,则可根据上述法则,通过反函数关系,将ψ(t)+C还原为F[ψ-1(x)]+C,从而得到所求的结果.这里选择ψ(t)的条件是:
容易求出,且等于ψ(t) +C,则可根据上述法则,通过反函数关系,将ψ(t)+C还原为F[ψ-1(x)]+C,从而得到所求的结果.这里选择ψ(t)的条件是:❶ψ(t)单调,可导,且+ψ′(t)≠0,以保证上述法则成立且被积函数f(x)的定义域不变.
❷要使∫f(ψ(t)]ψ′ (t)dt 容易求.
第二换元积分法用来求几种常见的无理函数的积分,十分方便.
❶若被积函数含有因子
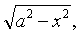 则可令x =asint或x =a c ost;
则可令x =asint或x =a c ost;❷若被积函数含有因子
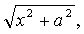 则可令x =atgt;
则可令x =atgt;❸若被积函数含有因子
 则可令x =aseet.
则可令x =aseet.例 求
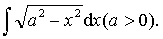
解 令x=asint,则ex=acostdt,t=aresin x/a. a
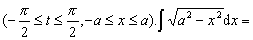
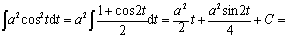
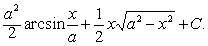
☚ 不定积分的第一换元积分法 分部积分法 ☛
- (1)止痛药是什么意思
- 1 正俗字是什么意思
- 1.武器种类是什么意思
- 1. 武威市是什么意思
- 1. 武当山风景名胜区是什么意思
- 1. 武汉市是什么意思
- (1)武装部队领导人是什么意思
- 1.母树林基地是什么意思
- 1.每百元生产性固定资产总收入是什么意思
- 1.每百元费用总收入是什么意思
- (1)比赛是什么意思
- (1)比赛、规则、裁判等是什么意思
- (1)比赛与阵势是什么意思
- (1)比赛用帆船是什么意思
- 1.毛纺是什么意思
- (1)毛纺与毛织工艺是什么意思
- 1.毛诗郑笺释兴是什么意思
- 1.民事是什么意思
- (1)民事权利是什么意思
- 1.民国时期是什么意思
- 1.民族是什么意思
- 1. 民族经济学的学科名称是什么意思
- 1.民航机构是什么意思
- (1)民航货运业务是什么意思
- (1)民航飞机类型是什么意思
- 1.民间歌曲是什么意思
- 1.气是什么意思
- 1.气候类型多样是什么意思
- 1.气压是什么意思
- 1.气温是什么意思
- 1.气温分布是什么意思
- 1. 氮肥是什么意思
- 1.水利工程是什么意思
- 1.水利建设是什么意思
- 1.水利建设投入是什么意思
- (1)水力发电工程是什么意思
- 1.水土流失严重是什么意思
- 1.水库养鱼是什么意思
- 1.水果是什么意思
- 1.水果产量居全国领先水平是什么意思
- (1)水果种类是什么意思
- 1.水环境质量是什么意思
- 1.水电站建设是什么意思
- 1.水电资源是什么意思
- 1.水磨加工是什么意思
- 1.水稻是什么意思
- 1.水稻技术推广是什么意思
- 1.水系分布是什么意思
- 1.水资源开发简史是什么意思
- 1.水资源贫乏且地区分布不均是什么意思
- 1.水运兴盛阶段是什么意思
- 1.水陆交通是什么意思
- 1. 汉中市是什么意思
- 1.汉中市草原工作站是什么意思
- 1 汉字对历代少数民族文字的影响是什么意思
- 1. 江川县是什么意思
- 1.江水北调是什么意思
- (1)江河是什么意思
- 1.江河是什么意思
- 1.江西农业大学是什么意思