一一对应yiyi duiying

设从集合A到集合B的映射是f:A→B，若在f的作用下，集合A中的不同元素在B中有不同的象，并且集合B中的每一个元素在集合A中都有原象，则称f为从A到B的一一对应，也称为一一映射(图1).

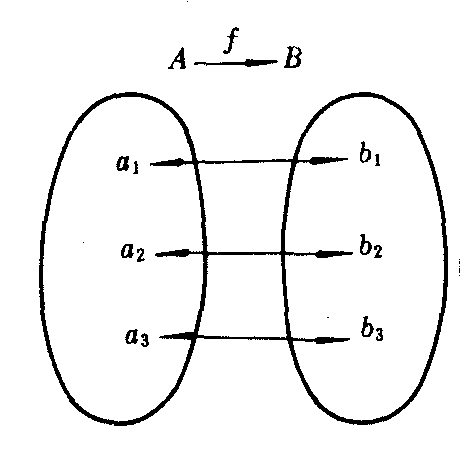
图1

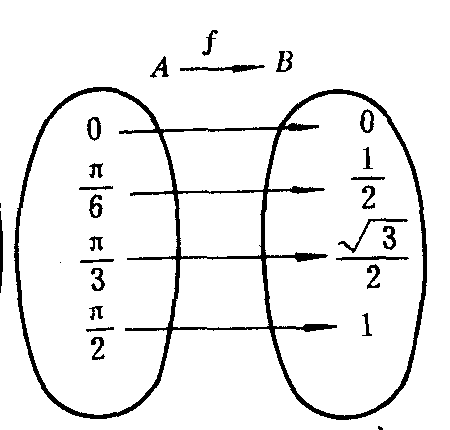
图2

一一对应的定义可以从下面三点来理解：
❶对于集合A中的每一个元素，必有集合B中的唯一元素和它对应；
❷A中不同的元素，不可能有B中的同一个元素和它们都对应；
❸B中的任何一个元素，在A中必有它的原象.
例如，假设集合A= {0,π/6,π/3,π/2),B=(0,1/2, /2,1}.则f:x→y=sinx (x∈A,y∈B)，就是从A到B的一一对应(图2).（林福智）

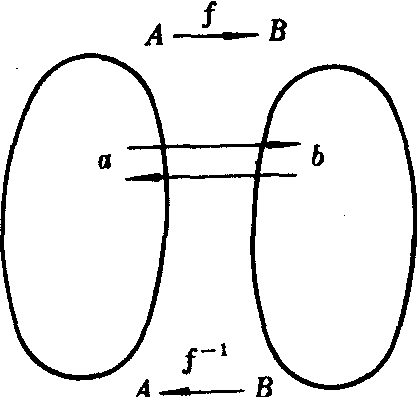
一一对应yiyi duiying

有两个集合A和B，如果集合A中的每一个元素都与B中唯一的一个元素对应，反过来，集合B中的每一个元素都与A中唯一的一个元素对应，则称A、B两个集合中的元素一一对应。幼儿的计数，比较两组物体的多少，都渗透了一一对应的思想。例如：幼儿按物点数，就是在自然数列与物体之间建立一一对应的关系。幼儿比较两组物体数量的多少，最初采用的办法就是采取对应的方法，将两组物体中的元素一一对应起来，比较数量的多少。

一一对应Yiyi duiying

给定两个集合A和B，如果按照某种对应关系，集合A的每一个元素， 都与集合B中的唯一确定的一个元素对应，同时集合B的每一个元素，也都与集合A中的唯一确定的一个元素对应，这样的对应关系叫做一一对应。在一一对应下，集合A中的不同元素在集合B中所对应的元素是不同的，而且，集合B的每一个元素都是集合A中某个元素的对应元素。例如，在条目“对应”中列举的四个图中只有 (1) 是一一对应。

一一对应

对于集A到B的映射，若A的不同元素有不同的象，且B的每个元素都有原象，称此映射为A到B的一一对应。例如，A和B分别是正、负整数全体所成的集，使每个正数a与-a相对应，就是A到B的一一对应。

---

一一对应

两集合间一种特殊的对应关系。满足：1.对于第一个集合中的任一元素，第二个集合中必存在一个且只存在一个元素与之对应；2.对于第二个集合中的任一元素，第一个集合中必存在一个且只存在一个元素与之对应。