t分布
如果随机变量X~N(0,1),Y~χ2(n),且X与Y相互独立,则随机变量t=![]() 的分布称为自由度是n的t分布,记为t(n)。常被应用于测验分数统计中。
的分布称为自由度是n的t分布,记为t(n)。常被应用于测验分数统计中。
t分布t-distribution,Student’s distribution
是数理统计中连续分布之一。t分布曲线是以0为中心的对称钟形曲线,曲线形状随着自由度v或(n-1)的大小而变化,自由度愈小,曲线顶部愈尖细而尾部愈粗宽,随着自由度的增大,t分布逐步逼近正态分布,自由度v=∞时,t分布即呈正态分布。实际工作中可应用t值表查得。
t分布
t分布是一种连续型分布,主要用于t检验及总体均数的区间估计等问题。W.S. Gosset于1908年以笔名“Student”发表了著名的t分布,开始了小样本研究的新纪元。因而t检验亦称Student t检验。
t为标准正态变量u与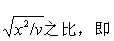
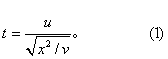

密度函数及其图形 t分布的密度函数为
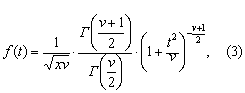
-∞
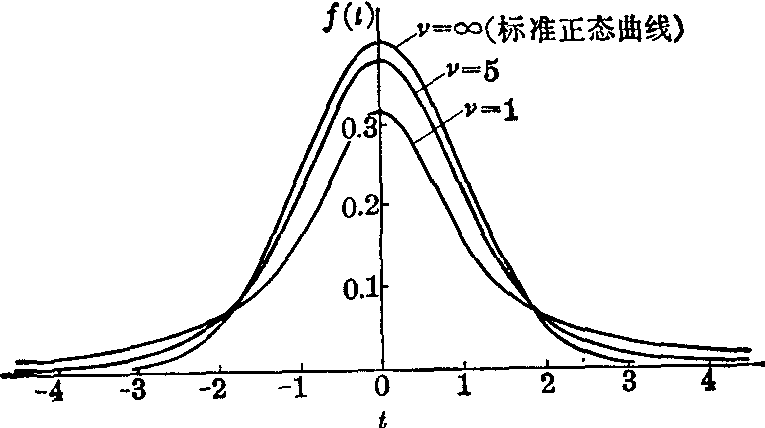
图1 不同自由度时的t分布曲线
图1说明,当v增大时,t分布逐渐逼近标准正态分布。t分布的分布函数为
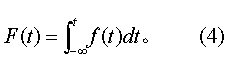
t分布的分位数 当v确定后,t分布曲线下,双侧尾部的面积P(2),或单侧尾部的面积P(1)为指定值α时,横轴上相应的界值t记为tα,v,如图2(b)。这就是t分布的分位数,此值有t界值表(如表)可查。作t检验时,
t分布的分位数表(t界值表)
| vP(1): P(2): | 0.250 0.500 | 0.100 0.200 | 0.050 0.100 | 0.025 0.050 | 0.010 0.020 | 0.005 0.010 |
| 1 2 3 4 5 | 1.000 0.816 0.765 0.741 0.727 | 3.078 1.886 1.638 1.533 1.476 | 6.314 2.920 2.353 2.132 2.015 | 12.706 4.303 3.182 2.776 2.571 | 31.821 6.965 4.541 3.747 3.365 | 63.657 9.925 5.841 4.604 4.032 |
| 6 7 8 9 10 | 0.718 0.711 0.706 0.703 0.700 | 1.440 1.415 1.397 1.383 1.372 | 1.943 1.895 1.860 1.833 1.812 | 2.447 2.365 2.306 2.262 2.228 | 3.143 2.998 2.896 2.821 2.764 | 3.707 3.499 3.355 3.250 3.169 |
| 11 12 13 14 15 | 0.697 0.695 0.694 0.692 0.691 | 1.363 1.356 1.350 1.345 1.341 | 1.796 1.782 1.771 1.761 1.753 | 2.201 2.179 2.160 2.145 2.131 | 2.718 2.681 2.650 2.624 2.602 | 3.106 3.055 3.012 2.977 2.947 |
| 16 17 18 19 20 | 0.690 0.689 0.688 0.688 0.687 | 1.337 1.333 1.330 1.328 1.325 | 1.746 1.740 1.734 1.729 1.725 | 2.120 2.110 2.101 2.093 2.086 | 2.583 2.567 2.552 2.539 2.528 | 2.921 2.898 2.878 2.861 2.845 |
| 21 22 23 24 25 | 0.686 0.686 0.685 0.685 0.684 | 1.323 1.321 1.319 1.318 1.316 | 1.721 1.717 1.714 1.711 1.708 | 2.080 2.074 2.069 2.064 2.060 | 2.518 2.508 2.500 2.492 2.485 | 2.831 2.819 2.807 2.797 2.787 |
| 26 27 28 29 30 | 0.684 0.684 0.683 0.683 0.683 | 1.315 1.314 1.313 1.311 1.310 | 1.706 1.703 1.701 1.699 1.697 | 2.056 2.052 2.048 2.045 2.042 | 2.479 2.473 2.467 2.462 2.457 | 2.779 2.771 2.763 2.756 2.750 |
| vP(1): P(2): | 0.250 0.500 | 0.100 0.200 | 0.050 0.100 | 0.025 0.050 | 0.010 0.020 | 0.005 0.010 |
| 31 32 33 34 35 | 0.682 0.682 0.682 0.682 0.682 | 1.309 1.309 1.308 1.307 1.306 | 1.696 1.694 1.692 1.691 1.690 | 2.040 2.037 2.035 2.032 2.030 | 2.453 2.449 2.445 2.441 2.438 | 2.744 2.738 2.733 2.728 2.724 |
| 36 37 38 39 40 | 0.681 0.681 0.681 0.681 0.681 | 1.306 1.305 1.304 1.304 1.303 | 1.688 1.687 1.686 1.685 1.684 | 2.028 2.026 2.024 2.023 2.021 | 2.434 2.431 2.429 2.426 2.423 | 2.719 2.715 2.712 2.708 2.704 |
| 41 42 43 44 45 | 0.681 0.680 0.680 0.680 0.680 | 1.303 1.302 1.302 1.301 1.301 | 1.683 1.682 1.681 1.680 1.679 | 2.020 2.018 2.017 2.015 2.014 | 2.421 2.418 2.416 2.414 2.412 | 2.701 2.698 2.695 2.692 2.690 |
| 46 47 48 49 50 | 0.680 0.680 0.680 0.680 0.679 | 1.300 1.300 1.299 1.299 1.299 | 1.679 1.678 1.677 1.677 1.676 | 2.013 2.012 2.011 2.010 2.009 | 2.410 2.408 2.407 2.405 2.403 | 2.687 2.685 2.682 2.680 2.678 |
| 60 80 120 240 ∞ | 0.679 0.678 0.677 0.676 0.674 | 1.296 1.292 1.289 1.285 1.282 | 1.671 1.664 1.658 1.651 1.645 | 2.000 1.990 1.980 1.970 1.960 | 2.390 2.374 2.358 2.342 2.326 | 2.660 2.639 2.617 2.596 2.576 |
摘自 山内二郎:統計数值表,30,JSA-1972
当求得观察样本的统计量t值后,按自由度v可由表查出单侧或双侧P值的大小。

图2 t分布曲线下的面积
用途
(1) t检验。可用于样本均数与总体均数的比较,两样本均数的比较等。适用条件是:当样本含量n较小时,要求样本取自正态总体。作两样本均数比较时,还要求经方差的齐性检验,两总体方差齐。
(2)总体均数的区间估计。
t分布tdistribution
亦称“学生分布”。统计推断的一种方法。在统计推断时,推断平均数一般都要用到总体方差,而多数情况下总体方差系未知数,须用样本方差代替,这就会导入误差,尤其在小样本时,误差有时会影响到必要的精确度。要克服此缺陷,须在计算公式中避免使用总体方差。1908年英国统计学家W.S.戈塞特以笔名“student”提出了t分布,该分布属于小样本的样本分配。当总体的σ2未知,抽取的样本个案数小于30时,其样本分配有特殊形式,称为t分布。特点为:对称、形态类似于正态曲线。t=0时对称,当n很大时,t分布近似于正态分布n (0,1)。在t分布中,表示其扩展程度的差异量数一般用标准误。用小样本组成的样本分布中,每个样本所处的位置用t值表示:t=(X-μ)/SE。t分布用于:(1)做总体平均数的估计; (2)做样本平均数与总体平均数差异显著性检验; (3)两个样本平均数差异的显著性检验;(4)平均量差异的估计。
t分布student's "t" distribution
亦称“学生分布”。在统计推断时,推断平均数一般都要用到总体方差,而多数情况下总体方差系未知数,须用样本方差代替,这就会导入一定的误差,尤其在小样本时,误差有时会影响到必要的精确度。为克服此缺陷,必须在计算公式中避免运用总体方差。考虑及此, 英国统计学家戈塞特(Gosset, W.S.)用“Student”为笔名提出了著名的t分布。t分布属于小样本的样本分配。当总体的σ2未知,抽取的又是小样本, 即个案数目小于 30时,其样本分配具有特殊的形式,统计学上称之为t分布。t分布为对称分布,形态类似于正态曲线。但t分布曲线两端较正态曲线为凸起。以t=0对称。当n很大时,t分布近似于正态分布n (0,1)。在t分布中,表示其扩展程度的差异量数一般用标准误差,亦为标准误。用小样本组成的样本分布中,每个样本所处的位置用r值表示:
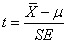
t分布的应用很广泛,主要有:(1)可用作总体平均数的估计。(2)可用作样本平均数与总体平均数差异显著性检验。(3)可用于两个样本平均数差异的显著性检验。(4)可用于平均量差异的估计。
t分布t-distribution
亦称“学生分布”。抽样分布的一种。英国统计学家戈塞特(William Sealy Gosset, 1876—1937)通过对大量数据的分析,以“学生分布”名义发表。左右对称,峰态比较高狭,分布形状随样本容量n-1的变化而变化,最终趋近于正态分布。推论统计发展里程碑之一,为小样本研究提供了理论依据。若总体服从
.jpg)
t分布
亦称“学生分布”。英国统计学家戈塞特(William Sealy Gosset, 1896—1937)通过对大量数据的分析,以“学生”名义所发表的一种左右对称,峰态比较高狭,分布形状随样本容量n-1的变化而变化的概率分布。推论统计发展里程碑之一。其概率密度函数为:
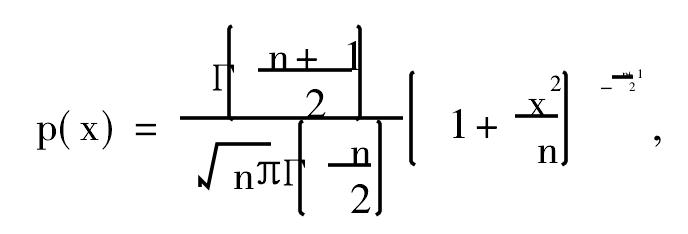
- 波丝呢是什么意思
- 波丝草是什么意思
- 波中峰一点,云际帆千片。是什么意思
- 波中猪是什么意思
- 波中猪(黑猪)是什么意思
- 波丹是什么意思
- 波么是什么意思
- 波义耳是什么意思
- 波义耳与子虚乌有的“微粒”是什么意思
- 波义耳定律是什么意思
- 波义耳-马略特定理是什么意思
- 波亚图是什么意思
- 波亚那教堂是什么意思
- 波亨斯基是什么意思
- 波什迦罗是什么意思
- 波仔是什么意思
- 波代诺内是什么意思
- 波伊提乌是什么意思
- 波伏瓦,西蒙娜是什么意思
- 波伐早熟禾是什么意思
- 波伦是什么意思
- 波伦亚是什么意思
- 波伦亚儿童读物博览会是什么意思
- 波伦亚画派是什么意思
- 波伦提亚之战是什么意思
- 波伦那储蓄银行是什么意思
- 波伯是什么意思
- 波佐利是什么意思
- 波佩耳征是什么意思
- 波依修斯是什么意思
- 波依斯征是什么意思
- 波依闊是什么意思
- 波依阔是什么意思
- 波俏是什么意思
- 波儿哈都台吉是什么意思
- 波光帆影是什么意思
- 波光摇海月 星影入城楼是什么意思
- 波光水鸟惊犹宿,露冷流萤湿不飞是什么意思
- 波光清澈明净是什么意思
- 波光滟滟前溪满,刹影亭亭古寺幽。是什么意思
- 波光粼粼是什么意思
- 波光连月 白,烛影到江红。是什么意思
- 波克罗夫斯克是什么意思
- 波克罗夫斯基是什么意思
- 波克罗夫村是什么意思
- 波克雷什金是什么意思
- 波兰是什么意思
- 波兰1791年宪法是什么意思
- 波兰1863年起义是什么意思
- 波兰1947年小宪法是什么意思
- 波兰一八六三年起义是什么意思
- 波兰七月宣言是什么意思
- 波兰三次被瓜分和复国是什么意思
- 波兰-东普鲁士战役是什么意思
- 波兰人是什么意思
- 波兰人民会议是什么意思
- 波兰人民共和国1952年宪法是什么意思
- 波兰人民共和国1976年宪法统一文本是什么意思
- 波兰人民共和国1983年宪法修正案是什么意思
- 波兰人民共和国1989年4月宪法修正案是什么意思