BCS理论BCS lilun

超导电性的微观理论。1911年发现超导电现象以后，人们一直在努力探索产生超导电性的微观机制。大量的实验事实表明，超导电性是由于电子气的行为发生某种深刻变化引起的，特点是无阻地运动。电子气处在这样高度有序的状态意味着电子之间的相互作用是吸引的。1950年发现的超导临界温度Tc的同位素效应，即Tc∞M-1/2^,M为同位素质量，表明尽管从正常态转变到超导态晶体结构不变，但晶格振动在造成电子气行为改变中必定起了重要的作用。1957年巴丁(J. Bardeen)、库伯(L.N. Cooper)和施里费(J. R.Schrieffer)提出了一种完整的超导电性微观理论，简称为BCS理论，它成功地解释了超导电性的起因及其重要性质。由它预言的结果与实验很好地符合。
BCS理论有两个基本概念：超导电性的起源是费米能面附近的电子之间存在通过交换声子而发生的吸引作用。这种吸引作用导致费米能面附近的电子两两结合成对，即构成所谓的库伯对；在结合成对时放出结合能，使电子体系的能量降低。可以按下面的简单图象来理解电子间通过交换声子而发生吸引作用，晶体（特别是导体）中电子是在由正离子组成的晶格环境中比较自由地运动的。带负电的电子吸引它周围的正离子向它靠拢，所以在电子周围形成正电荷相对积聚的区域，而原来的电子发生了状态变化。该正电区域又吸引附近的第二个电子。这样，第一个电子由于晶格正离子的移动而间接地吸引了第二个电子。正离子的微小移动必然以波的形式传给整个晶格，产生晶格振动，即发射了声子。因此，两个电子间的间接吸引作用实质上是通过声子来实现的。例如动量和能量分别为p₁和ε(p₁)的电子与晶格的相互作用发射出动量为hq的声子，电子动量和能量变为p′1=p1-hq和ε(p′1)。而能量和动量分别为ε(p₂)和p₂的电子正好吸收了这个声子，能量和动量变为ε(p′2)、p_′2=p₂+hq。这种情形的结果是一对电子之间发生了能量和动量的交换，也就是通过交换声子使两个电子之间间接地发生了作用。根据量子力学的测不准原理，在这样一种过程中，作为中间过程的声子发射和吸收可以不服从能量守恒定律。理论计算表明，当每一个电子前后状态的能量差小于声子能量时，电子间的这种间接相互作用是吸引的。考虑到泡利不相容原理，费米能面以下深处的能态已为电子占满，它们难以吸收或发射声子，而同能级相近的电子发生作用。只有在费米能面附近的电子之间才能存在间接吸引作用。这一部分是呈现超导电性的电子。间接吸引作用的强弱，取决于一对电子〔ε(p₁),p₁〕、〔ε(p₂),p₂〕通过交换声子可以转变过去的状态〔ε(p′₁),p′1〕、〔ε(p′₂),p′₂〕的多寡。所以，在费米能面附近动量等大反向、自旋相反的一对电子〔p₁＝p₂↑,p₂＝-p↓,ε(p₁)≈ε(p₂)≈εF（即费米能量）〕之间存在着比其他情形都要强的吸引作用。如果电子间的这种吸引作用超过了库仑斥力作用，就会使 一对p↑、-p↓的电子结合成电子对，即库伯对，因为这样不仅会使电子气的能量下降到低于正常费米分布时的能量，而且这样结合成的束缚态电子对的能量最低，使电子体系的基态能量最小。
在库伯对的基础上建立起来的BCS理论认为：
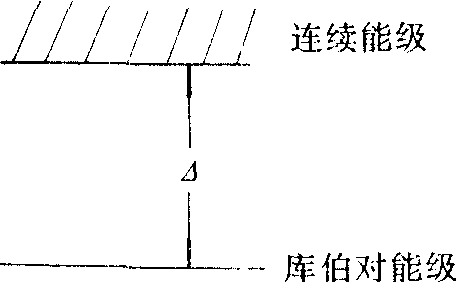
❶费米能面附近的电子两两结合成库伯对，改变了这些电子的能谱，使得在连续谱的能带态以下出现一个单独的能级，即库伯对的能量状态——超导体中的电子能谱，如图所示。库伯对能级与连续能级之间的间隔为Δ,Δ称为超导体的能隙。所以把一个库伯对拆散成不相关的两个电子，至少要给予一定的能量，其值为库伯对的结合能2Δ，即至少要给予每个电子的能量为Δ。计算结果表明，电子能谱的连续部分也发生了变化，电子能量不是正常状态下的ε(p)，而是。 此外，对应于各种能量的状态数目也与正常状态时的不同。超导电子就是构成库伯对的那些电子。在绝对零度，费米能面附近的所有电子都构成库伯对，因而超导态是一种高度有序的状态。每个库伯对都可以看成是一个复合粒子，其总的自旋为零，遵守玻色统计规律（而正常态的电子遵守费米统计规律）。这种体系的基态是所有库伯对都处在具有相同能量的量子态中，可用同一波函数描述每一个库伯对。利用测不准关系可以估计出一个库伯对中两个电子之间的距离大约为10-6米，即大约是晶格常数的104倍。这一方面说明库伯对是一个很松的体系，其结合能2Δ实际上是很小的，一般只有毫电子伏特的数量级。另一方面也说明了库伯对之间必定互相交叉重叠，存在着较强的相互作用，从而使超导态的电子表现出整体的协同性。实际上，可以直观地把库伯对的大小看成是一个库伯对可以跟其它库伯对“直接地”发生相互作用的范围，在BCS理论中则称为超导相干长度。
❷吸引作用、库伯对和能隙，都是电子气的集体效应。由于一对电子(p↑,-p↓)间吸引作用的强弱，取决于允许它们变过去的状态(p′↑,-p′↓)的多寡。假设费米能面附近存在一些未成对的电子(P₁↑,-p₂↓)等，由于泡利不相容原理禁止电子对(p↑,-p↓)转变到状态(p₁↑,-p₁↓)、(p₂↑,-p₂↓)等去，减弱电子对(p↑,-p↓)间的吸引作用。于是，一个库伯对内部的吸引作用的强弱，库伯对的结合能或超导体的能隙Δ的大小，取决于费米能面附近全部电子的状态分布。当费米能面附近的电子全都两两结合成对时，Δ最大。拆散一个或数个库伯对，则剩下的每个库伯对的结合也变得更加松弛。在T=OK时，费米能面附近的所有电子都结合成库伯对，这个状态为超导基态，能隙大小为

式中，ωD是德拜频率，g(εF)是正常状态下费米能面处的电子状态密度，V为电子间的有效相互作用矩阵元。在T≠0K时，晶格振动可以把一些库伯对拆散变成正常电子，所以，温度愈高库伯对愈少，正常电子愈多，Δ愈小。到T=Tc时，所有电子都是正常电子，Δ=0。Δ与温度有关，为

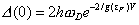
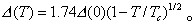
❸根据BCS理论中的能隙方程，临界温度可以表示为

由于ωD∝M-1/2，所以得出了同位素效应。此外g(εF)V越大，Tc就越高。V大意味着电子与声子的耦合强，有利于超导态的形成。但V大亦意味着在正常状态下导体的电阻大。所以不良导体更容易出现超导态。
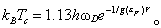
❹超导体内没有电流时，每个库伯对的总动量都为零，即p+(-p)=0。而当超导体处于载流的超导态时，每个库伯对的总动量不再为零，所有库伯对都具有同一动量P，电流由这些库伯对运送。交换声子的散射过程只使得这一库伯对转化为具有同一动量的另一个库伯对，因而超导电流不会衰减，这就是无阻电流的机理。唯一能使超导电流衰减的过程是将库伯对拆散的那种散射过程。但这种过程所需的能量至少应等于2△。在电流密度比较低的情形下是无法提供这么大的能量的，因此拆散库伯对的散射是禁止的。由此可知，超导体所运载的超导电流存在一个最大值，称临界电流。当流过超导体的电流超过这一值时，就能提供足够的能量破坏库伯对，使超导体转变为正常导体。
❺由BCS理论可以导出与伦敦方程、皮帕德方程以及金茨堡—朗道方程相似的方程，可以解释大量的超导现象和实验事实，所以BCS理论是一个较成功的理论。只是近来高温超导体的出现，才又对理论提出了新的要求。