18世纪数学shiba shiji shuxue

17世纪的数学的延续.虽然没有提供17世纪那样众多新颖而基本的概念与思想，却施展了高超的技巧，并根据力学与天文学的需要，提出与解决了大量的新问题.在数学方法上则完成了从几何方法向解析方法的转变.
这个世纪最引人注目的是微积分发挥出巨大的威力，产生了无穷级数、常微分方程、偏微分方程、变分法等重要分支，从而建立了现代数学中最广阔的一个领域——数学分析.这些进展主要是在贝努利家族、泰勒、欧拉、克雷罗、达朗贝尔、拉格朗日等人的推动下完成的.对微积分本身，17世纪末约翰·贝努利得到了确定0/0型不定式的所谓洛必大法则.1712年泰勒提出了泰勒级数.1742年，麦克劳林给出了它的特殊情形——麦克劳林级数，但实际上它早已出现在泰勒的著作中.1718年，约翰·伯努利首先从解析的角度定义了函数概念，以后又经欧拉之手，使之进一步深化.1748年，欧拉的《无穷小分析引论》的出版标志着微积分发展的一个新阶段.在此之前，主要由方丹、欧拉、克雷罗、达朗贝尔等人开创了偏导数理论.在此以后，则以欧拉、拉格朗日为主开展了对多重积分的研究.
在无穷级数方面，继牛顿、泰勒之后，欧拉做了广泛的研究，1747年探讨了三角级数，在级数收敛性方面，1713年莱布尼兹提出了交错级数收敛的充分条件是|an|→0;1742年麦克劳林提出了积分判别法.在微积分初创时期常微分方程已经出现，但主要的进展开始于18世纪，大量著名的微分方程被引入，并逐渐开展了对解的系统研究；微分方程组研究也于1750年以后由欧拉、拉格朗日、拉普斯等人所开创.偏微分方程最初于1734年出现在欧拉的著作中，而其第一次真正的成功始于1746年达朗尔对弦振动问题的重新研究，并在18世纪后半叶被推广.1772年，拉格朗日研究了非线性一阶偏微分方程的一般理论.1696年，约翰·贝努利提出了著名的最速降线问题和解法并得到推广(欧拉，1734年)，导致了变分法的诞生.18世纪的变分法主要是由拉格朗日推动的.
与分析领域的巨大成就相比，其他领域的发展略为逊色，但仍有许多是极为重要的.首先是概率论，1713年，雅各·贝努利的遗著《猜变术》出版，这是概率论的第一部专著，对早期概率论做了全面总结，给出了大数定律.紧接着，德莫弗尔在《机会论》(1718年)、《分析杂论》(1730)中给出了大量新内容，包括概率乘法公式、概率积分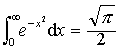、在统计学中重要的正态频率曲线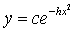，以及在当n很大时的公式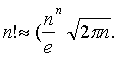.1777年，法国人蒲丰提出了著名的“投针问题”，开始了几何概率的研究.
18世纪，解析几何与微分几何的进展交织在一起.1704年，牛顿发表《三次曲线》，研究了78种可能情形中的72种.1715年，约翰·贝努利引入了三个坐标面.1731年，克雷罗开创了空间曲线理论，是三维微分几何的第一个重大进展.此后，欧拉对解析几何、空间曲线与曲面理论都有重要贡献，包括曲线的参数表示，一般二次曲线的分类，曲线奇点，曲线、曲面上测地线的微分方程等，特别是1760年在《关于曲面上曲线的研究》中建立了曲面的理论.18世纪末至19世纪初，经过蒙日及其学生们的努力，终于把微分几何做为一门独立的学科建立起来.这方面的奠基性著作是他的《分析在几何学上的应用》，同时他还是画法几何的奠基人.
在代数学方面，对五次以上代数方程公式解的探讨仍在继续.线性方程组的研究经麦克劳林、克莱默的工作，在贝佐特手中系统化，给出了代数消元法的一般理论.1772年，范德蒙德首次对行列式理论作出了独立而连贯的逻辑阐述.1799年，高斯证明了代数基本定理，在此之前，欧拉、达朗、贝尔、拉格朗日都做过努力.
18世纪的数论主要是由欧拉推动的.他证明了费尔马提出的许多数论命题，包括费尔马小定理，n=3和4时的费尔马大定理，费尔马两平方定理等.他给出了62对亲和数(其中有2对是错的)，提出了二次互反律，这是18世纪数论中最富创造性的成果，于1801年被高斯证明，并称之为“算术中的宝石”.1742年，1770年，哥德巴赫与华林分别提出了他们著名的猜想成为后世数论中的重大课题.
18世纪的数学在迅速发展的同时也暴露出其弱点：忽略了数学方法与基础的严密性，从而导致了一系列矛盾，而18世纪的数学家对此似乎并不十分担心，人们坚信，在物理学上的正确性保证了它在数学上的正确性.

18世纪数学18shiji shuxue

与17世纪相比，18世纪的数学虽然没有提供那样众多新颖而基本的概念与方法，却施展了高度的技巧，并根据科学技术特别是力学与天文学的需要， 提出和解决了大量新的问题。在数学方法上则完成了从几何方法向解析方法的转变。
这个世纪最引人注目的是微积分的迅速发展并发挥出巨大威力。一些重要概念（如函数）被不断明确和深化，一些强有力的方法被建立， 18世纪中叶， 多元微积分的概念与方法也已初步建立。1748年，欧拉出版了《无穷小分析引论》，标志着微积分发展的一个新阶段，与此同时，微积分向更加广阔的领域扩展，产生了无穷级数、常微分方程、偏微分方程、变分法等重要分支， 从而使现代数学中最广阔的领域——数学分析初具规模。这些进展主要是在伯努利家族、泰勒(Taylor. B.)、欧拉、克莱罗 (Clairaut, A. C.)、达朗贝尔、拉格朗日、拉普拉斯等人的推动下实现的。
与分析领域的巨大成就相比，其他领域略为逊色，但仍有十分明显的进步。
1713年，雅各布·伯努利的遗著《猜度术》出版，这是概率论的第一部专著， 对早期概率论作了全面总结。随后， 棣莫弗在 《机会论》 (1718)、《分析杂论》(1730) 中给出了大量新内容。1777年， 法国人蒲丰(Buffon, G. L. L.)提出了著名的 “投针问题”， 开始了几何概率的研究。
解析几何的进步与微分几何的创建交织在一起。1704年， 牛顿发表 《三次曲线》， 研究了78种可能情形中的72种。1715年，约翰·伯努利引入了三个坐标面， 1731年， 克莱罗开创了空间曲线理论，是三维微分几何的第一个重大进展。此后，欧拉对解析几何、空间曲线与曲面理论都有重要贡献。18世纪末至19世纪初，经过蒙日及其学生们的努力，终于把微分几何作为一门独立的学科建立起来， 同时他还是画法几何的奠基人。
在代数学方面， 对五次以上代数方程根式解的探讨仍在继续，其中拉格朗日的工作对19世纪群论的诞生有着重要意义。线性方程组及行列式已经建立了独立而系统化的理论。1799年， 高斯继承欧拉、达朗贝尔、拉格朗日的工作，终于给出了代数基本定理的第一个证明。
18世纪的数论主要是由欧拉推动的，他证明了费尔马提出的许多数论命题，系统地探讨了亲和数，并提出了二次互反律，这是18世纪数论中最富创造性的成果， 于1801年被高斯证明， 并称之为 “算术中的宝石”。哥德巴赫(1742) 与华林(Waring, E, 1770)分别提出了他们的著名猜想， 成为后世数论中的重大课题。18世纪后期，拉格朗日、勒让德也有重要的工作。
18世纪的数学在迅速发展的同时也暴露出其弱点：忽略了数学方法与基础的严密性，从而导致了一系列矛盾， 而18世纪的数学家对此似乎并不十分担心。这一时期的数学家大多又是物理学家，人们坚信，概念与方法在物理学上的正确性保证了它们在数学上的正确性。