消费者需求基本矩阵方程
假定效用函数u(x)是二次连续可微分的,x∈X是消费丛,需求函数ψ(p,ω)定义为
ψ(p,ω)={x∈Xpx≤ω,若px′≤W则x=x′或非x′=x}
其中价格p和财富ω是预先给定的.那么经典最大化问题max{u(x)x∈X,px=ω}的解就是x0=ψ(p,ω)。
考虑对应的拉格朗日函数,由极值的一阶条件得到
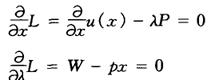
对应于解x0=ψ(p,ω),可以解出λ的解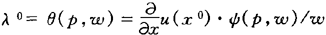 。用U表示u的海赛矩阵,U0为U在x0=ψ(p,ω)的值,一阶条件就化为
。用U表示u的海赛矩阵,U0为U在x0=ψ(p,ω)的值,一阶条件就化为
U0dx-λ0dp-pdλ=0
dω-pdx-x0dp=0
写成矩阵形式就是
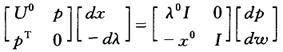
其中I是单位矩阵(K阶),这就是消费者需求基本矩阵方程。
- 疯狂地舞动是什么意思
- 疯狂地逃窜是什么意思
- 疯狂地闹是什么意思
- 疯狂地骂是什么意思
- 疯狂战争是什么意思
- 疯狂爵士乐演奏者是什么意思
- 疯狂病是什么意思
- 疯狂的君子兰是什么意思
- 疯狂的奥尔兰多是什么意思
- 疯狂的时刻 [阿尔及利亚]狄布是什么意思
- 疯狂的比尔· 希科克是什么意思
- 疯狂的猴子是什么意思
- 疯狂的石头是什么意思
- 疯狂英语是什么意思
- 疯狂螺丝钉是什么意思
- 疯狂行为是什么意思
- 疯狗是什么意思
- 疯狗咬人——不看对象是什么意思
- 疯狗咬人——死不松口是什么意思
- 疯狗咬人无药医是什么意思
- 疯狗咬伤是什么意思
- 疯狗咬月亮是什么意思
- 疯狗咬月亮——狂妄(汪)是什么意思
- 疯狗咬月亮——狂汪(妄)是什么意思
- 疯狗头上长犄角——凭空多了一路招数是什么意思
- 疯狗扬长是什么意思
- 疯狗狾狗是什么意思
- 疯狗的脾气是什么意思
- 疯狗的脾气——见人就咬是什么意思
- 疯狗跳墙头是什么意思
- 疯狼跑进了羊群里——乱得没法儿收拾是什么意思
- 疯猴是什么意思
- 疯疯傻傻是什么意思
- 疯疯势势是什么意思
- 疯疯子是什么意思
- 疯疯张张是什么意思
- 疯疯扯扯是什么意思
- 疯疯癫癫是什么意思
- 疯疯癫癫,精神不正常是什么意思
- 疯疯颠颠是什么意思
- 疯病是什么意思
- 疯痨臌胀膈,阎王请下客是什么意思
- 疯痨臌膈,阎罗王请的上客是什么意思
- 疯痨臌隔,是阎罗王请到的上客。是什么意思
- 疯瘫是什么意思
- 疯癫是什么意思
- 疯癫愚昧是什么意思
- 疯癫痴呆是什么意思
- 疯癫痴呆的样子是什么意思
- 疯癫的人是什么意思
- 疯癫识倒是什么意思
- 疯癫,受到某种精神刺激而精神失常是什么意思
- 疯的是什么意思
- 疯着心是什么意思
- 疯笑是什么意思
- 疯草是什么意思
- 疯蒙是什么意思
- 疯蚂蚁是什么意思
- 疯话是什么意思
- 疯语是什么意思