标准差的计算

---

对某量x₀在相同条件下多次独立测得

x₁，x₂，…，x_n

则计算单次测量标准差σ可用如下方法。

1．贝塞尔法

对第i次测量而言，其误差

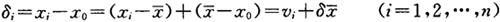
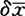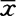式中v_i为第i次测量的残差，为平均值的误差。

将各式平方和，得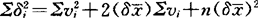

两端除n，注意

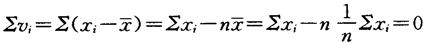
得

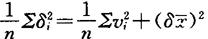
平均值误差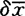可用其标准差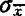代替，因

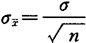
式中σ为单次测量标准差，故

这就是贝塞尔公式，此法算标准差即为贝塞尔法，它由残差

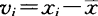
可算单次测量标准差σ及平均值标准差

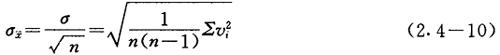
〔例2．4－6〕 对某物理量独立测9次，得值

则其最佳值

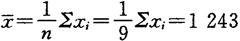
算出各次测量值x_i的残差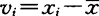如上，于是由贝塞尔公式，单次测量标准差

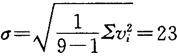
平均值标准差

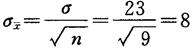
2．彼得斯法

对样本平均误差

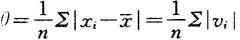
可算出其期望

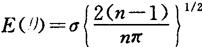
于是单次测量标准差

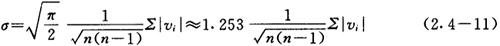
此即彼得斯公式，它可由v取绝对值求和以算出σ。

〔例2．4－7〕 测量所得值同例2．4－6，按彼得斯公式

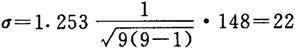
3．极差法

对极差

w_n=maxx_i－minx_i

可求得其期望

Ew_n=d_nσ

而单次测量标准差

式中d_n的数值如表2．4－1。

表2．4－1 极差d_n表

〔例2．4－8〕 测量所得值同例2．4－6，按极差法，因

w₉=1258－1189=69

由n=9查上表得d_n=2．97，故

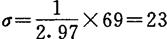
4．最大误差法

有时，可以预先知道某量的约定真值，从而可在多次独立测量后，算出误差δ_i，因max｜δ_i｜的期望

E(max｜δ_i｜)=K_nσ

故单次测量标准差

式中1／K_n的数值如表2．4－2。

表2．4－2 最大误差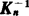表

〔例2．4－9〕 在30t处用检衡车检轨道衔10次，读数为

因检衡车30t是高精度测得的，可视作真值，于是上述读数与30t之差即为误差，而

max｜δ_i｜=15kg

从而

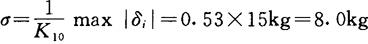
5．最大残差法

对各次残差v₁，v₂，…，v_n，找出max｜v_i｜，因期望

E(max｜v_i｜)=K′_nσ，故单次测量标准差

式中1／K′_n的数值如表2．4－3。

表2．4－3 最大残差Kn^－1表

〔例2．4－10〕 对某量测4次，得

1．70，1．57，1．37，1．71

则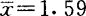，因

max｜v_i｜=0．22

故

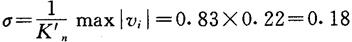
6．分组极差法

对某量独立测m组，每组n次，得

x_1(j)，x_2(j)，…，x_n(j)，(j=1，2，…，m)

算各组极差

w₍₁₎，w₍₂₎，…，w_(m)

平均极差

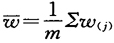
而单次测量标准差

式中c值如表2．4－4。

表2．4－4 分组极差c值表

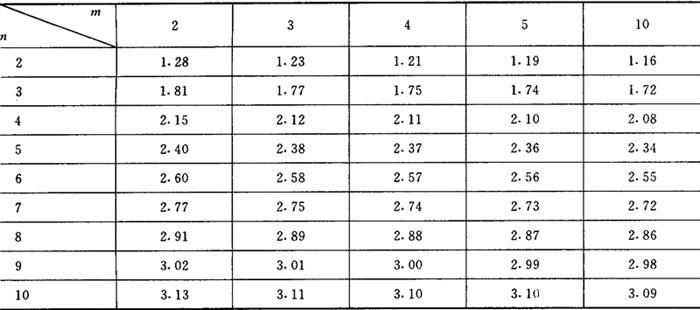
〔例2．4－11〕 只对某量独立测m=10组，每组测n=3次，各组极差分别为

w₍₁₎=0．063 w₍₆₎=0．080

w₍₂₎=0．077 w₍₇₎=0．043

w₍₃₎=0．068 w₍₈₎=0．055

w₍₄₎=0．066 w₍₉₎=0．029

w₍₅₎=0．047 w₍₁₀₎=0．047

平均极差

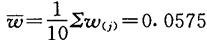
而单次测量标准差

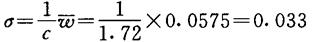
【参考文献】：

［1］王立吉，计量学基础，中国计量出版社，1988。

［2］BIPM、IEC、IFCC，IUPAC，IUPAP，OIML，Guide to the Expression of Uncertainty in Measurement， ISO，1993．

［3］刘智敏，不确定度原理，中国计量出版社，1993。

［4］刘智敏，误差分布论，原子能出版社，1988。

［5］刘智敏，误差与数据处理，原子能出版社，1983。

［6］Liu Zhimin(刘智敏)，Measurement Uncertainty and Its Correlation Combination，Proceeding of ISEM， 1993．

［7］国家计量总局量值传递处编，计量技术考核纲要，计量出版社，1981。

［8］国家技术监督局审定，刘智敏等编审，全国计量检定人员考核统一试题集第六分册三，误差及数据处理，陕西科学技术出版社，1990。