极大线性无关组、向量组的秩

---

极大线性无关组 向量组α₁，α₂，…，α_s，若存在部分组α_i1，α_i2，…，α_ir线性无关，α₁，α₂，…，α_s中任一向量均可由α_i1，α_i2，…，α_ir线性表示，则称α_i1，α_i2，…，α_ir是向量组α₁，α₂，…，α_，的极大线性无关组．

或向量组α₁，α₂，…，α_s的部分组α_i1，α_i2，…，α_ir线性无关，再添加进组中的任一向量α_i(如果还有的话)都线性相关，则称α_i1，α_i2，…，α_ir是向量组α₁，α₂，…，α_s的极大线性无关组．

只有零向量构成的向量组设有极大无关组．

一个线性无关向量组的极大线性无关组就是向量组本身．

向量组的秩 向量组α₁，α₂，…，α_s中极大线性无关组向量的个数，称为向量组的秩，记为r(α₁，α₂，…，α_s)．

等价向量组 若向量组(Ⅰ)α₁，α₂，…，α_s中任一向量都可由向量组(Ⅱ)β₁，β₂，…，β_t线性表示，则称向量组(Ⅰ)可由向量组(Ⅱ)线性表示．若向量组(Ⅰ)，(Ⅱ)可以相互表示，则称这两个向量组等价，记作．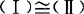

有关等价向量组的一些重要结论

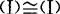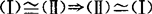(1)向量组的等价关系具有反身性，对称性和传递性，设向量组(Ⅰ)α₁，…，α_s，(Ⅱ)β₁，…，β_t，(Ⅲ)γ₁，γ₂，…，γ_p，则①．②若．③若，．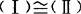

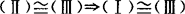(2)任一向量组与其极大线性无关组等价．

(3)向量组的极大无关组不惟一，同一个向量组的两个极大无关组等价，且向量个数相同．

(4)两个线性无关向量组等价，则它们的向量个数相同．

(5)等价向量组等秩，即对于(Ⅰ)α₁，α₂，…，α_s，(Ⅱ)β₁，β₂，…，β_t，若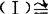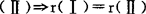．反之不成立．

向量组的秩和矩阵的关系

(1)矩阵的行秩，列秩：矩阵A_m×n按列分块，A=(α₁，α₂，…，α_n)，则r(α₁，α₂，…，α_n)称为A的列(向量组的)秩；按行分块，，则r(β₁，β₂，…，β_m)称为A的行秩．

(2)三秩相等：设A_m×n，则r(A)=A的行秩=A的列秩．

(3)被表示的向量秩小：向量组(Ⅰ)α₁，α₂，…，α_s可被向量组(Ⅱ)β₁，β₂，…，β_t线性表示，则

r(α₁，α₂，…，α_s)≤r(β₁，β₂，…，β_t)．

(4)初等变换不改变矩阵的秩．

(5)A，B是同型矩阵，则．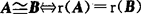

(6)向量组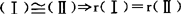，反之不成立．

矩阵秩的重要公式

(1)A_m×n，则r(A)≤m；r(A)≤n；r(A)≥0．

(2)r(A)=r(A^T)．

(3)r(A+B)≤r(A)+r(B)．

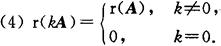
(5)r(AB)≤r(A)，当B可逆，或B的行向量线性无关时，等号成立；r(AB)≤r(B)，当A可逆或A的列向量组线性无关时，等号成立．

(6)A_m×n，B_n×s，则r(AB)≥r(A)+r(B)－n．

(7)若A_m×n，B_n×s，且AB=0，则r(A)+r(B)≤n．

向量组的极大线性无关组，向量组秩的求法

方法1：将向量组处理成行向量，且合并成矩阵A，对A做初等行变换，且化成阶梯形矩阵，不妨设

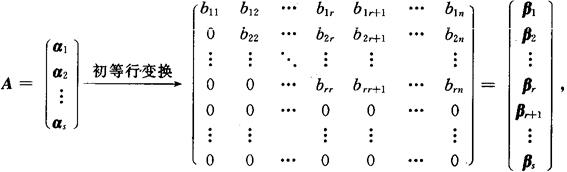
则

(1)向量组α₁，α₂，…，α_s与β₁，β₂，…，β_s可以相互表示，是等价向量组，等价向量组等秩，从而α₁，α₂，…，α_s与β₁，β₂，…，β_s有相同的线性相关性．

(2)阶梯形向量β₁，β₂，…，β_r线性无关(β_j=0，j=r+1，…，s)，是β₁，β₂，…，β_s的极大线性无关组．设β₁，β₂，…，β_r可由α_i1，α_i2，…，α_ir线性表示，则α_i1，α_i2，…，α_ir和β₁，β₂，…，β_r也是等价向量，α_i1，α_i2，…，α_ir是α₁，α₂，…，α_s的极大线性无关组，r(α₁，α₂，…，α_s)=r．

(3)β_j(k=r+1，r+2，…，s)是零向量(若存在)，若

βj=k₁α_i1+k₂α_i2+…+k_rα_ir+k_r+1α_l=0

则

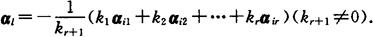
例 已知α₁=(1，－1，2，4)^T，α₂=(0，3，1，2)^T，α₃=(3，0，7，14)^T，α₄=(2，1，5，10)^T，α₅=(1，－2，2，0)^T．求α₁，α₂，α₃，α₄，α₅的极大线性无关组和秩，并将其余向量由极大线性无关组线性表示．

解 将α₁，α₂，α₃，α₄，α₅处理成行向量，合并成矩阵，做初等行变换，并记下所做变换，化成阶梯形矩阵．

β₁，β₂，β₃，β₄，β₅中极大无关组是β₁，β₂，β₃，r(β₁，β₂，…，β₅)=3，故α₁，α₂，α₃，α₄，α₅的极大无关组是α₁，α₂，α₅，r(α₁，α₂，α₃，α₄，α₅)=3，β₄=α₃－3α₁－α₂=0，α₃=3α₁+α₂，β₅=α₄－2α₁－α₂=0，α₄=2α₁+α₂．

方法2：将向量组处理成列向量组，合并成矩阵，做初等行变换，化成阶梯形矩阵，设

A=(α₁，α₂，…，α_s)→B=(β₁，β₂，…，β_s)，

则

(1)α₁，α₂，…，α_s与β₁，β₂，…，β_s具有相同的线性相关性(方程组(α₁，α₂，…．α_s)X=0与(β₁，β₂，…，β_s)X=0是同解方程组)．

(2)α₁，α₂，…，α_s与β₁，β₂，…，β_s中任何对应的列向量组具有相同的线性相关性(对应的列向量组组成的齐次方程组是同解方程组)．

(3)若β_i可由β_i1，β_i2，…，βi_r线性表出，则α_i可由α_i1，α_i2，…，α_ir线性表示．((β_i1，β_i2，…，β_ir)X=β_i与(α_i1，α_i2，…，α_ir)X=α_i是同解方程组)．

(4)β_i1，β_i2，…，βi_r是β₁，β₂，…，β_s的极大无关组，则α_i1，α_i2，…，α_ir是α₁，α₂，…．α_s的极大线性无关组．