曲面积分的定义、性质和计算

---

对面积(或第一型)的曲面积分定义 设曲面∑是光滑⁽¹⁾的，函数f(x，y，z)在∑上有界．将∑任分为几小块△Si．同时也代表第i块曲面的面积，在∑上任取一点(ξ_i，η_i，ξ_i)(i=1，2，…，n)作和式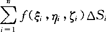i．如果当小块曲面的直径最大值λ→0时，和式的极限存在，则称此极限为函数f(x，y，z)在曲面S上的对面积(或第一型)的曲面积分．记作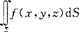即

其中f(x，y，z)称为被积函数，f(x，y，z)dS称为被积分式，∑称为积分曲面．

对面积的曲面积分的性质(见图11．7)

图11．7

对面积的曲面积分的计算公式 设曲面∑由z=z(x，y)给出，∑在Oxy平面上的投影区域为D．z=z(x，y)在D上具有连续偏导数，f(x，y，z)在∑上连续，则

类似可得，曲面∑由x=x(y，z)给出，∑在Oyz平面的投影区域为D，则

曲面∑在Ozx平面的投影区域为D，∑由y=y(x，z)给出，则

对坐标曲面积分的定义 设∑为光滑有向曲面，函数R(x，y，z)在∑上有界．将∑任分成n个小有向曲面△S_i(也表示第i块小曲面的面积)．△Si在Oxy面上的投影为(△S_i)_xy，(ξ_i，η_i，ξi)是△S_i任取的一点．如果当各小块曲面的直径的最大值λ→0时，

存在，则称此极限为函数R(x，y，z)在有向曲面∑上对坐标x，y(第二型)的曲面积分，记作‖R(x，y，z)dxdy，即

其中R(x，y，z)称为被积函数，∑称为积分曲面．

类似地，可定义函数P(x，y，z)在有向曲面∑上对坐标y，z(第一型)的曲面

组合曲面积分

对坐标的曲面积分的性质

其中－∑表示与∑方向相反的有向曲面．

Q(x，y，z)dzdx+R(x，y，z)dxdy．

对坐标的曲面积分的计算方法

(1)当曲面方程以z=z(x，y)给出时，

其中z(x，y)具有一阶连续偏导数，∑在Oxy面上的投影为D_xy．当有向曲面∑取上侧时，则公式中取正号，取下侧时，则公式中取负号．

(2)若曲面∑的方程以y=y(x，z)给出，且有一阶连续偏导数，∑在Oxz面上的投影为D_xz，则

当有向曲面∑取右侧时，公式中取正号；∑取左侧时，公式取负号．

(3)若曲面方程以x=x(y，z)给出，且具有一阶连续偏导数，∑在Oyz平面上的投影为D_yz，则

当有向曲面∑取前侧时，公式中取正号；∑取后侧时，公式中取负号．

两类曲面积之间的关系

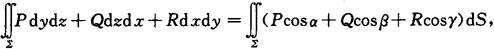
其中cosα，cosβ，cosγ是有向曲面S上点(x，y，z)处的法向量的方向余弦．