微分法在几何上的应用

---

空间曲线的切线与法平面方程

切向量 曲线上点M处切线的方向向量称为曲线的切向量(见图9．3)．

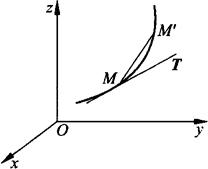
图9．3

法平面 过曲线上的点M且与切线垂直的平面称为法平面．

(1)设空间曲线的方程为

曲线在M处的切线方程为

切向量为T=｛φ′(t₀)，ψ′(t₀)，ω′(t₀)｝．曲线在M处的法平面方程为

φ′(t₀)(x－x₀)+ψ′(t₀)(y－y₀)+ω′(t₀)(z－z₀)=0．

(2)设空间曲线方程为

在点M(x₀，y₀，z₀)处的切线方程为

切向量为T=｛1，φ′(x₀)，ψ′(x₀)｝．曲线在M处的法平面方程为

(x－x₀)+φ′(x₀)(y－y₀)+ψ′(x₀)(z－z₀)=0．

(3)空间曲线方程为

曲线在M处的切线方程为

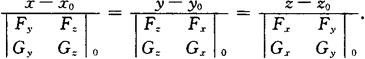
曲线在M处的法平面方程为

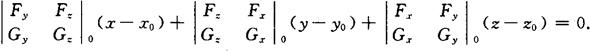
空间曲面的切平面与法线方程

法线 通过点M(x₀，y₀，z₀)而垂直于切平面的直线称为曲面在该点的法线．

法向量 垂直于曲面上切平面的向量称为曲面的法向量(见图9．4)．

图9．4

(1)设空间曲面的方程为F(x，y，z)=0，曲面在点M处的切平面方程为

F_x(x₀，y₀，z₀)(x－x₀)+Fy(x₀，y₀，z₀)×(y－y₀)+F_z(x₀，y₀，z₀)(z－z₀)=0．

曲面在点M处的法线方程为

曲面在M处的法向量为

n=｛F_x(x₀，y₀，z₀)，F_y(x₀，y₀，z₀)，Fz(x₀，y₀，z₀)｝．

(2)空间曲面的方程为z=f(x，y)，曲面在点M处的切平面方程为

fx(x₀，y₀)(x－x₀)+f_y(x₀，y₀)(y－y₀)=z－z₀．

曲面在M处的法线方程为

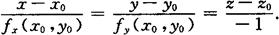
方向余弦 若α，β，γ表示曲面法向量的方向角，并假定法向量的方向是向上的，即使得它与z轴的正向所成的角γ是锐角，则法向量的方向余弦为

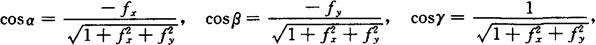
其中

f_x=f_x(x₀，y₀)，f_y=f_y(x₀，y₀)．

方向导数 函数的增量f(x+△x，y+△y)－f(x，y)与PP′两点间的距离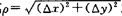之比值，当P′沿着l趋于P时，如果此比的极限存在(如图9．5)，则称这极限为函数在点P沿方向l的方向导数，记为

图9．5

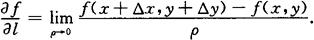
特别地，函数f(x，y)在点P沿着x轴正向e₁=｛1，0｝、y轴正向e₂=｛0，1｝的方向导数分别为f_x，f_y；沿着x轴负向、y轴负向的方向导数是－f_x，－f_y．

对于三元函数u=f(x，y，z)，它在空间一点P(x，y，z)沿着方向L的方向导数，可定义为

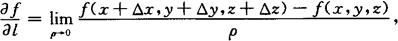
其中

定理 如果函数z=f(x，y)在点P(x，y)是可微分的，那么函数在该点沿任意方向l的方向导数都存在，且有

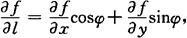
其中φ为x轴到方向l的转角．

如果函数u=f(x，y，z)在点P(x，y，z)是可微分的，那么函数在该点沿任意方向l的方向导数都存在，且有

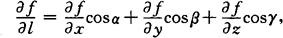
其中方向l的方向角为α，β，γ．

梯度 设函数z=f(x，y)在平面区域D内具有一阶连续偏导数，则对于每一点P(x，y)∈D，都可定出一个向量这向量称为函数z=f(x，y)在点P(x，y)的梯度，记为

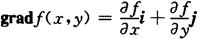
函数在某点的梯度的方向与取得最大方向导数的方向一致，它的模为方向导数的最大值，即

当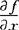不为零时，x轴到梯度的转角的正切为

设函数u=f(x，y，z)在空间区域G内具有一阶连续偏导数，则对于每一点P(x，y，z)∈G，梯度

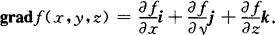
等高线 曲线

称为函数z=f(x，y)的等高线．

梯度与等高线的关系 函数z=f(x，y)在点P(x，y)的梯度的方向与点P的等高线f(x，y)=c在这点的法线的一个方向相同，且从数值较低的等高线指向数值较高的等高线，而梯度的模等于函数在这个法线方向的方向导数．

等量面 曲面f(x，y，z)=c(c为常数)为函数u=f(x，y，z)的等量面．

梯度与等量面的关系 函数u=f(x，y，z)在点P(x，y，z)的梯度的方向与过点P的等量面f(x，y，z)=c在这点的法线的一个方向相同，且从数值较低的等量面指向数值较高的等量面，而梯度的模等于函数在这个法线方向的方向导数．