二元函数的泰勒公式
定理 设z=f(x,y)在点(x0,y0)的某一邻域有直到n+1阶的连续偏导数,(x0+h,y0+k)为此邻域内任一点,则二元函数f(x,y)在点(x0,y0)的n阶泰勒公式为
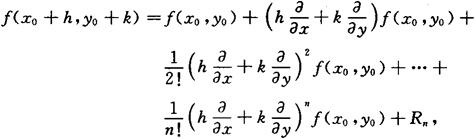
其中
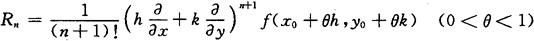
称为拉格朗日型余项.记号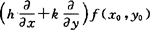 表示
表示
hfx(x0,y0)+kfy(x0,y0),
(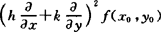 表示
表示
h2fxx(x0,y0)+2hkfxy(x0,y0)+k2fyy(x0,y0).
一般地,记号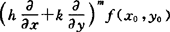 表示
表示
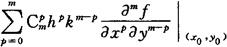
误差估计式
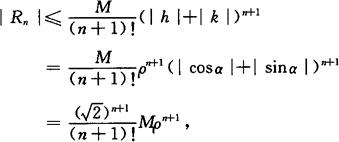
其中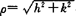 ,M为函数z=f(x,y)在点(x0,y0)处的(n+1)阶偏导数的界.
,M为函数z=f(x,y)在点(x0,y0)处的(n+1)阶偏导数的界.
误差|Rn|是当ρ→0时比ρn高阶的无穷小.
当n=0时,由二元函数f(x,y)在点(x0,y0)的n阶泰勒公式就是二元函数的拉格朗日中值公式:
f(x0+h,y0+k)=f(x0,y0)+hfx(x0+θh,y0+θk)+kfy(x0+θh,y0+θk).
推论 如果函数f(x,y)的偏导数fx(x,y),fy(x,y)在某一邻域内都恒等于零,那么函数f(x,y)在该区域内为一常数.
二元函数n阶麦克劳林公式 在二元函数f(x,y)在点(x0,y0)的n阶泰勒公式中,若取x0=0,y0=0,则得n阶麦克劳林公式:
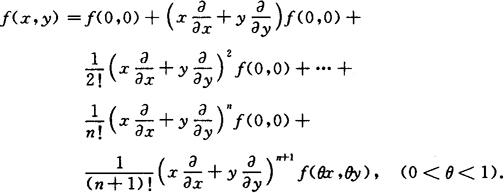
- 人月圆令是什么意思
- 人月圆 客垂虹 - 元·张可久是什么意思
- 人月圆 (明)杨慎是什么意思
- 人月圆 - 金·吴激是什么意思
- 人月圆(伤心莫问前朝事)是什么意思
- 人月重圆是什么意思
- 人有一技之长,不愁家无米粮是什么意思
- 人有一技之长,不愁家里无米粮是什么意思
- 人有一技之长,不愁家里无粮是什么意思
- 人有一艺,终身可靠是什么意思
- 人有七分怕鬼是什么意思
- 人有七贫八富是什么意思
- 人有三不幸,少年登高科,一不幸;席父兄之势为美官,二不幸;有高才,能文章,三不幸也。是什么意思
- 人有三不幸:少年登高科,一不幸;席父兄之势为美官,二不幸;有高才能文章,三不幸也。是什么意思
- 人有三不祥,曰盈,曰矜,曰争。盈则倾,矜则凌,争则刑。惟盈故矜,惟矜故争。是什么意思
- 人有三分怕虎,虎有七分怕人是什么意思
- 人有三分怕鬼,鬼有七分怕人是什么意思
- 人有三成人: 知畏惧,成人;知羞耻,成人;知艰难,成人是什么意思
- 人有三昏三迷是什么意思
- 人有三灾六难是什么意思
- 人有三父八母是什么意思
- 人有三衰六旺是什么意思
- 人有不为也,而后可以有为是什么意思
- 人有不为也,而后可以有为。是什么意思
- 人有不为也,而后可以有为(《孟子·离娄下》)是什么意思
- 人有不善,则乃性命之疾也,无其教治而欲令变更,岂不难哉!是什么意思
- 人有两只脚,银子有八只脚是什么意思
- 人有了心病,猫叫也心惊是什么意思
- 人有亏心事,肚内不安宁是什么意思
- 人有亏心,天必不容是什么意思
- 人有五事令人常肥。一者数食,二者喜眠,三者憍乐,四者无忧,五者无事。是什么意思
- 人有亡斧者是什么意思
- 人有亡斧者,意其邻之子是什么意思
- 人有亡鈇者是什么意思
- 人有亡鈇者,疑其邻之子,视其行步,窃鈇也;颜色,窃鈇也;言语,窃鈇也;动作态度,无为而不窃鈇也。是什么意思
- 人有人不同,花有几样红是什么意思
- 人有人之是非,事有事之是非,而人与事之是非,心里直下分明, 只此是智。是什么意思
- 人有人言,兽有兽语是什么意思
- 人有人语,马有马情是什么意思
- 人有人门,狗有狗窦是什么意思
- 人有几等人,佛有几等佛是什么意思
- 人有几等人,物有几等物,宝有几等宝,活也有几等活是什么意思
- 人有前后眼,富贵一千年是什么意思
- 人有十不同,花有十样红是什么意思
- 人有十年旺,神鬼不敢傍是什么意思
- 人有十等是什么意思
- 人有千年誉,花无百日红是什么意思
- 人有千算,天只一算是什么意思
- 人有卒然祸福是什么意思
- 人有厚德,无问小节;人有大举,无訾小故是什么意思
- 人有厚德,无问小节;人有大举,无訾小故。是什么意思
- 人有古怪相,必有古怪能是什么意思
- 人有可延之寿,亦有可折之寿是什么意思
- 人有可延之寿, 亦有可折之寿。是什么意思
- 人有吉凶事是什么意思
- 人有吉凶事,不在鸟音中是什么意思
- 人有同貌人,物有同形物是什么意思
- 人有名,树有影是什么意思
- 人有善愿,天必从之是什么意思
- 人有喜庆不可妒忌,人有祸患不可喜幸。是什么意思