X2检验法

---

这是非参数的假设检验，是对总体分布进行假设检验．

设总体X的实际分布函数为F(x)，它是未知的．从样本值推测出的可能的总体X的分布函数为F^*(x)，并称F*(x)为X的理论分布函数，然后对F^*(x)进行检验．

具体检验方法如下：

(1)将n个样本值按大小顺序排列并等分成k个小区间(每个小区间内的样本点数不要小于5个)，用mi表示在第i个小区间［t_i－1，t_i］上的样本值个数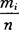，为频率，画出频率的直方图，从直方图估出总体X的分布，定出X的分布函数F^*(x)．

原假设 H₀：F(x)=F^*(x)．

设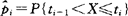，在H₀成立的条件下，有

pi=F^*(t_i)－F^*(t_i－1)．

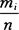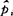研究与的差异程度．或说是m_i与n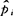的差异程度．

(2)选统计量

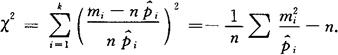
皮尔逊(Pearson)证明了当n→+∞时，X²的极限分布是X²(k－r－1)分布，其中r是F^*(x)中待估参数的个数．当n充分大(一般n≥50)时，就按X²(k－r－1)分布处理．

(3)对给定的α，小概率事件的概率表达式为．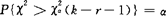

(4)由样本值求出X²值，查出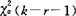的值．

(5)判断：若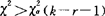，小概率事件出现，则拒绝H₀；若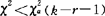，则接受H0：F(x)=F^*(x)．