高斯求积法

---

如何利用函数f(x)在某些点上的函数值，给出积分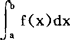的近似值，这是个数值积分问题。

高斯求积公式是数值积分中最常用的公式之一。

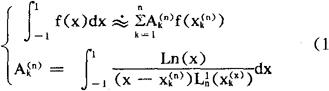
就是高斯求积公式。这里的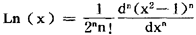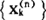，是它的n个根。在实际计算时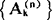，及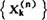都可通过查表给出，然后代入(1)式即可。

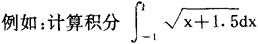
给出表格如下

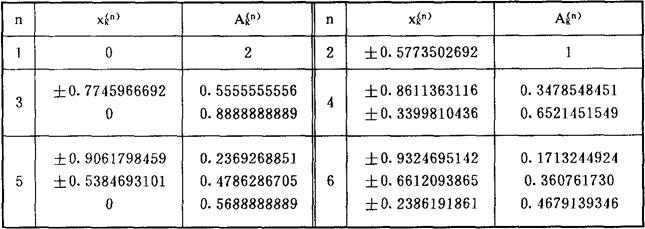
用两点高斯求积公式，则得 (2)

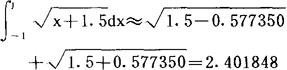
若用三点高斯求积公式，则得

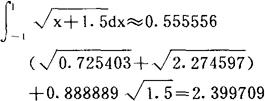
此积分的精确值为。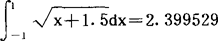

高斯求积公式计算稳定且具有较高的精确度，当f(x)是次数≤2n－1次多项式时，(1)是精确成立的。

如果积分区间是〔a，b〕，可先通过变量替换化为〔－1，1〕上的积分：

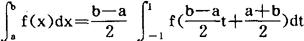
然后再利用高斯求积公式。