求实对称矩阵的全部特征值及特征向量的有效方法。
从理论上讲,任何对称矩阵A都可以通过正交相似变换,化为对角形RTAR=A。A的对角元素,就是A的诸特征值,而R的诸列就是A的特征向量。雅可比方法是通过有限次镜像变换(正交相似变换)把矩阵的主对角线以外的每个元素的绝对值都变得很小,这样变换后的矩阵就近似一对角阵,其对角元素就可作为A的近似特征值。
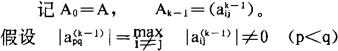
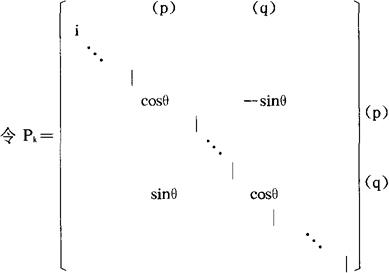
它与单位矩阵的差别,仅在第p,q行与第p,q列的交叉元素上,其中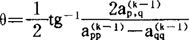 ,
,
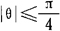
定义变换前后矩阵之间的关系为:

直止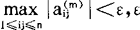 ,ε为允许精度,此时就有
,ε为允许精度,此时就有
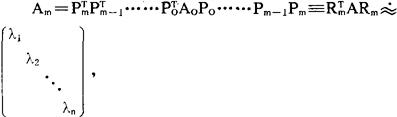
而Rm=P0Pi……Pm的第i列就是对应于λi的近似特征向量。
实际计算时,Ak及Rk按下列公式进行递推:

令R0=I,因为Rk=Rk-1Pk,
故有
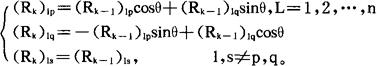
- 做集是什么意思
- 做雨是什么意思
- 做雨天是什么意思
- 做雪是什么意思
- 做零工是什么意思
- 做零工的人是什么意思
- 做零活儿的报酬是什么意思
- 做零活,打短工是什么意思
- 做霉是什么意思
- 做霜是什么意思
- 做霜构是什么意思
- 做青是什么意思
- 做非凡之事是什么意思
- 做面是什么意思
- 做面做目是什么意思
- 做面子是什么意思
- 做面孔是什么意思
- 做面皮是什么意思
- 做面目是什么意思
- 做面线是什么意思
- 做鞋是什么意思
- 做鞋佬是什么意思
- 做鞋则是什么意思
- 做项是什么意思
- 做顺水人情是什么意思
- 做顺莫是什么意思
- 做领袖要学会隐藏恐惧是什么意思
- 做额子是什么意思
- 做风是什么意思
- 做风做涌是什么意思
- 做风台是什么意思
- 做风水是什么意思
- 做风灾是什么意思
- 做食是什么意思
- 做食品的猪羊大肠是什么意思
- 做饭是什么意思
- 做饭个是什么意思
- 做饭做菜是什么意思
- 做饭厦是什么意思
- 做饭哩是什么意思
- 做饭处是什么意思
- 做饭姐是什么意思
- 做饭婆是什么意思
- 做饭嫂是什么意思
- 做饭屋是什么意思
- 做饭庵娘是什么意思
- 做饭烧菜是什么意思
- 做饭生的烟是什么意思
- 做饭用的柴和米是什么意思
- 做饭的是什么意思
- 做饭的人是什么意思
- 做饭瞒不了锅台,挑水瞒不了井台是什么意思
- 做饭菜及厨房里的相关工作是什么意思
- 做饭菜的房屋是什么意思
- 做饭那儿是什么意思
- 做饭酒铺是什么意思
- 做饺子是什么意思
- 做饽饽揉黄连——自找苦是什么意思
- 做馆是什么意思
- 做馍剂儿是什么意思