配镜处方及其转换

---

一镜片处方如果含有散光的话，可以写成多种形式。一般而言，处方的球镜屈光度可选择两个主子午线轴的任何一个屈光度，这样，另一轴向即为散光度数。用图解法来分析十分简单，这种图解称为“光学十字线”(optical cross)。

镜片图(lenS diagram)或光学十字线含有两条互相垂直的主子午线，每一条子午线标明了该线条上的屈光度(不是轴向)。在垂直线的上端，标明子午线的轴向(用度表示)，在同一垂直线的下端标明该子午线的屈光度；在水平线的左端，标明该子午线的轴向(用度表示)，在线的右端标明它的屈光度。举例说明，图2－29(1)表示的处方为：

+1．00D球镜(sph)联合(comb)+1．00D柱镜(cy1)轴向(ax)90°

球镜屈光度标明在两条子午线上，而柱镜的屈光度标明在180°子午线上(散光轴90°)。因此，在180°子午线上的总屈光度为球镜与柱镜屈光度之和。同样，屈光度也可用图2－29(2)表示，其处方形式为：

+2．00D球镜联合－1．00D柱镜轴向180°

验光配镜处方的规范写法为：

+2．00DS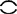－1．00DC×180°

任何镜片处方都可以在光学十字线上表达。平柱镜片相对球柱镜来说，它的球镜屈光度是0。比如：－3．00D柱镜轴向180°的镜片，同样也可处方为：－3．00D球镜联合+3．00D柱镜轴向90°。

镜片可以做成不同的形状，也就是说，在镜片的背面加工柱镜，也可在镜片的前面加工柱镜。两镜片的物理形状不同，其光学性能也有一定的区别，但是在处方意义上其屈光度是一致的。保持镜片的屈光度而改变其理论上的形状或处方形式称为转换(tranSposition)。

一片+1．00D的球镜片可被考虑为两片单柱镜片的组合，即+1．00D轴向90°联合+1．00D轴向180°。一片单柱镜片可以被转换成一片球柱镜，如+1．00D柱镜轴向180°，可以转换成+1．00D球镜联合－1．00D柱镜轴向90°。

两片单柱镜片可以转换成一片球柱镜片，其方法是首先将一片单柱镜片转换成球柱镜片，再加上第二片单柱镜片。如一片为+1．00D柱镜轴向90°，另一片为+2．00D柱镜轴向180°。将第一片转换为+1．00D球镜联合－1．00D柱镜轴向180°，再加上第二片镜片，结果为+1．00D球镜联合+1．00D柱镜轴向180°。

一球柱镜处方可通过下述简单的规则转换为另一种球柱镜处方形式。

(1)将球镜屈光度与柱镜屈光度的代数和作为新的球镜屈光度。

(2)将原柱镜的相反符号作为新柱镜的符号。

(3)原柱镜轴向度数加上90°或减去90°作为新柱镜轴向度数。

例如+1．00D球镜联合－2．00D柱镜轴向180°，可以改为－1．00D球镜联合+2．00D柱镜轴向90°。