3.4.1 惯性力和惯性力系的简化
质点在惯性空间以加速度a运动,则定义质点的惯性力为
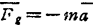 (其中m为质点的质量) (1.2-48)
(其中m为质点的质量) (1.2-48)
质点系中各质点的惯性力所组成的惯性力系可以向任一简化中心简化,得到一个等效的惯性力和惯性力偶。该惯性力的矢量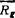 等于原惯性力系的主矢,且可写为
等于原惯性力系的主矢,且可写为
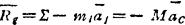
式中 M为质点系的总质量;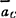 为质点系的质心加速度。该惯性力的大小和方向与简化中心无关。简化得到的惯性力偶,其矩等于原惯性力系对简化中心的主矩,该惯性力偶矩的大小和方向随简化中心选取的变化而将发生改变。
为质点系的质心加速度。该惯性力的大小和方向与简化中心无关。简化得到的惯性力偶,其矩等于原惯性力系对简化中心的主矩,该惯性力偶矩的大小和方向随简化中心选取的变化而将发生改变。
刚体作平动、定轴转动和平面运动时,其上各点惯性力系简化结果见表1.2-23。
表1.2-23 刚体惯性力系的简化结果
解:1.以曲杆和转轴为研究对象;2。对象所受已知力有转动力偶矩M、CD、DE的重力P1=P2=mg;约束反力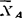 、
、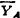 、
、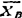 、
、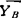 ;3.CD的惯性力G1、DE的惯性力G2分别在它们的对称面内,且
;3.CD的惯性力G1、DE的惯性力G2分别在它们的对称面内,且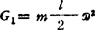 ,G2=mlω2;4.建立图示坐标,有平衡方程:
,G2=mlω2;4.建立图示坐标,有平衡方程:
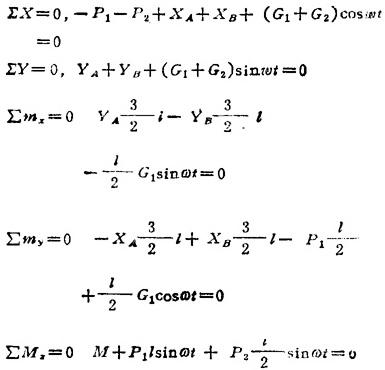
解方程并代入G1、G2之值便可得
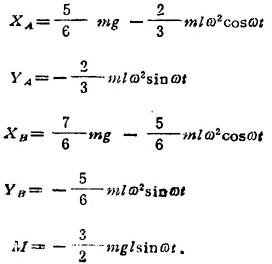
- 吴朝辉是什么意思
- 吴朝鸿是什么意思
- 吴木泉是什么意思
- 吴末帝是什么意思
- 吴末帝(孙皓)是什么意思
- 吴本勇是什么意思
- 吴本田是什么意思
- 吴本立是什么意思
- 吴本立是什么意思
- 吴札听歌而美其风是什么意思
- 吴机鹏是什么意思
- 吴村水柜是什么意思
- 吴杜炎是什么意思
- 吴来峰是什么意思
- 吴来金是什么意思
- 吴杰是什么意思
- 吴杰是什么意思
- 吴松寿是什么意思
- 吴松山是什么意思
- 吴松林是什么意思
- 吴松龄是什么意思
- 吴林是什么意思
- 吴林生是什么意思
- 吴枝新是什么意思
- 吴枢是什么意思
- 吴枫是什么意思
- 吴柳生是什么意思
- 吴柳生是什么意思
- 吴树人是什么意思
- 吴树声是什么意思
- 吴树威是什么意思
- 吴树森是什么意思
- 吴树民是什么意思
- 吴树达是什么意思
- 吴树青选集是什么意思
- 吴根茂是什么意思
- 吴格是什么意思
- 吴格是什么意思
- 吴桂华是什么意思
- 吴桂显是什么意思
- 吴桂纺是什么意思
- 吴桂芳是什么意思
- 吴桂英是什么意思
- 吴桐森是什么意思
- 吴桓兴是什么意思
- 吴桓兴是什么意思
- 吴桢是什么意思
- 吴桥是什么意思
- 吴桥县志是什么意思
- 吴桥教案是什么意思
- 吴桥杂技是什么意思
- 吴桥案是什么意思
- 吴桥街道是什么意思
- 吴桭臣是什么意思
- 吴梅是什么意思
- 吴梅是什么意思
- 吴梅是什么意思
- 吴梅是什么意思
- 吴梅是什么意思
- 吴梅是什么意思