线性方程组

---

6．2．1 含n个未知量n个方程的线性方程组解法

含n个未知量n个方程的线性方程组

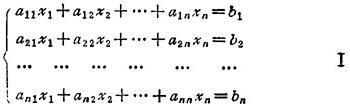
当常数项b₁，b₂，…b_n不全为零时，I称为非齐次线性方程组；当b₁，b₂，…b_n全为零时，I称为齐次线性方程组。

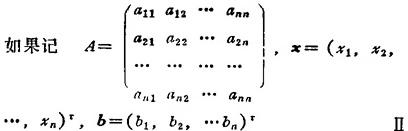
则线性方程组Ⅰ可写成矩阵形式Ax=b。

逆矩阵解法：当|A|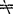0时，线性方程组Ⅱ的解为x=A^－1b，式中A^－1是系数矩阵A的逆矩阵，x称为Ⅱ的解矢量。

克莱姆法则：若|A|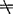0，则方程组Ⅰ的解为

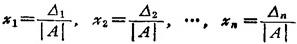
式中 △₁，△₂，…，△_n分别为以常数项矢量b代换系数矩阵A中第i列矢量后得到的n阶行列式。

工程中常用的有如下近似解法：

一是高斯消去法(主元素消去法)，对于n阶线性方程组

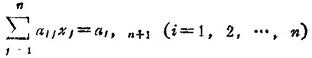
消元求解的步骤为：

❶ 在系数矩阵中找出绝对值最大的元素(主元素)，一般设a11为主元素(可换位获得)。将第一个方程乘以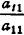－，分别与第t个方程相加，得到新

的n阶线性方程组。

❷ 在除第一行外的系数矩阵找出主元素，一般设b22为主元素，再将第二个方程乘以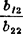－分

别与第i个方程相加(i=3，4，…n)，得到新的n阶线性方程组。

❸ 按照❶ 、❷ 的方法进行n－1次以后，消元过程结束，原来的系数矩阵已经化为上三角矩阵(未知量的次序也经过了若干次调换)。

❹ 由第n个方程解出xn。将xn代入第n－1个方程，解出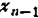，…，最后将已解出的x₂，x₃，…，x_n代入第一个方程解出x1。

二是赛德尔迭代法。其一般步骤为：

❶ 将线性方程组

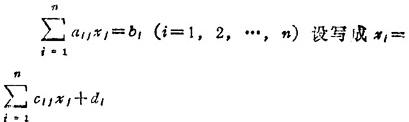
❷ 任选一组初始值x¹⁽⁰)⁾，x₂^《0)⁰⁾，…x_n⁽⁰⁾作为方程的第0次近似解。

❸ 依次使k=1，2，3…，用公式

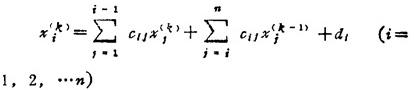
求出方程的第k次近似解，直到满足给定精度ε为止。

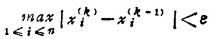
三是松弛迭代法。其基本步骤与第二种方法相同，只是把其中的第❸ 步的迭代公式改为

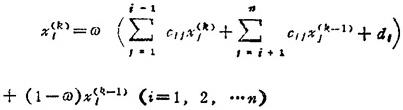
6．2．2 线性方程组有解的判别定理

对于含n个未知量m个方程的线性方程组，以r(A)，r(C)分别表示系数矩阵A和增广矩阵C的秩，则：

当m=n且r(A)=r(C)=n(或|A|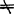0)时，方程组有唯一解。

当r(A)＜r(C)时，方程组无解，称为矛盾方程组。

当r(A)=r(C)=r＜n(或|A|=0)时，方程组有无穷多组解。

齐次线性方程组有非零解的充要条件是r(A)＜n，即|A|=0。

6．2．3 线性方程组的解的结构

当r(A)=r＜n时，齐次方程组Ax=0的任一非零解x=(x₁，x₂，…，x_n)^t都可用它的n－r个线性无关解x⁽¹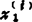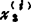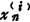⁾=(，，…，)^r(i=1。2，…，n－r)的线性组合来表示。这n－r个线性无关解称为方程组的基础解系，它不是唯一的。

设x⁽⁰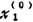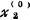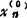⁾=(，，…，)r是线性方程组Ax=b的一个特解，则它的任一解x=(x1，x2，…x_n)r都可表示为x=x⁽⁰⁾+η。其中η=(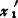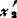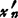，，…，)是它相应的齐次方程组Ax=0的一个解。