线性支出系统

---

英国经济学家斯通所提出的一种关于消费支出的经济模型。

该模型中的消费函数都是线性函数，故得名。具体模型如下：

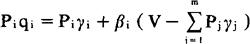
i=1，2，3，…。

在上式中，V是消费总支出，包括商品支出和服务支出，共分成m个类别；P_i是第i类商品或服务的价格；q_i是对第i类商品或服务的消费量；γ_i是对第i类商品或服务的基本消费需求量，可以看作是既定时期和既定的社会条件下满足生存需求的最低限额；P_iγ_i是对第i类商品或服务的基本消费需求支出额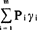，_i(i可用j代换)就

是全部基本消费需求支出总额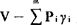；是总支出中扣除基本消费需求支出总额后余下的消费支出，叫作剩余支出。

它将按照β_i(i=1，2，3，…，m)的份额分别追加到各分类消费中。

β_i就叫做第i类消费的预算份额。显然有：

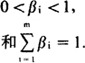
Piq_i是对第i类消费需求的支出额，等于基本消费需求额p_iγ_i与追加额β_i(V－∑P_jγ_j)之和。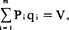。这一系统把分类消费支出p_iq_i看作总支出和价格的函数，γ_i和β_i(i=1，2，…，m)是待估计的参数。

这个模型在西方经济学界得到广泛应用，但如果缺少价格资料则无法估计出参数，这是该模型的一大缺点。

〔参〕 扩展的线性支出系统