种群增长模型

---

探讨种群数量变动最初使用的数字模型是指数增长曲线。

这个模型假定某种群生活在最优越的生活环境中，食物和栖息场所无限广阔，没有任何天敌或流行病。模型的方程式为。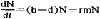

积分得：

Nt=N₀e^rmt其中b=种群的瞬时出生率，d=种群的瞬时死亡率，rm=b－d，为种群瞬时增长率，以t为时间，N为种群内个体数。N₀=开始时种群内个体数，Vt=在时刻t时种群内个体数，e=自然对数的底数。

上面的微分方程通过对数变换成为直线方程式为InNt=InN₀+rmt 例如在大肠杆菌的培养基中，接种每毫升1000个大肠杆菌，经2小时后，增长到38，000个／毫升，由此可以计算出大肠杆菌此时的瞬时增长率为：

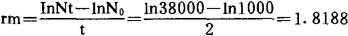
由瞬时增长率计算出每小时后，由一个大肠杆菌繁殖出的菌数为：InNt=InN₀+rmt=In1+1．8188×1=1．8188查对数表得Nt=6．1645即每小时平均可以由一个大肠杆菌分裂为6．1645个大肠杆菌，如果用繁殖曲线表示，就成为J型曲线，即种群数量成直线上升。

但指数增长必竟在自然界难以实现，因为很多自然种群的数量增长往往会受空间和食物的限制，种群密度对于种群数量的增长，一般表现为反馈式的影响。

即随著种群密度增长，种群数量增长的速度将会逐步下降。种群密度N达到极限K值(环境容纳量)时，种群增长将趋近于零。

这就是种群数量增长的逻辑斯谛曲线数学模型的依据。这种模型将种群增长的空间和食物上的限制概括进去了。这与指数增长模型显然改进了一步。

逻辑斯谛增长的原理可以下列微分方程表达：

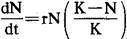
式中K是环境容纳量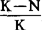，表示增长速度将随种群密度加大而减慢的一种参数。

当N等于K值时，种群不再增长。上式积分后即可得

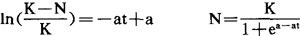
其中a是积分常数，由于逻辑斯谛公式的二阶导数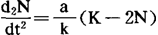，故在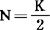时，曲线有控

点。即在种群数量增长中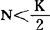，时，增长是以加速方式进行。在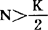时，则以逐步减速的方式增长，所以逻辑斯谛曲线是一条S型的曲线。

在自然界中，许多生物种群的增长符合这个模型，如细菌，果蝇乃至人类。