直角三角形边角关系的实际应用

---

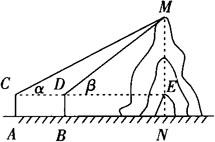
例1 如图，在小山的东侧A庄，有一热气球，由于受西风的影响，以每分钟35m的速度沿著水平方向成75°角的方向飞行，40分钟时到达C处，此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上，同时测得B庄的俯角为30°，又在A庄测得山顶P的仰角为45°，求A庄与B庄的距离及山高．(保留准确值)

解 (1)正确画出示意图．

(2)
❶ 在测点A处安置测倾器，测得此时山顶M的仰角∠MCE=α；

❷ 在测点A与小山之间的B处安置测倾器(A、B与N在同一条线上)，测得此时山顶M的仰角∠MDE=β；

❸ 量出测倾器的高度AC=BD=h，以及测点A、B之间的距离AB=m，根据上述测量数据，即可求出小山的高度MN．

例13 如图：某船以每小时36海里的速度向正东方向航行，在A点测得某岛C在北偏东60°的方向上，航行半小时后到B点测得该岛在北偏东30°方向上，已知该岛周围16海里内有暗礁．(1)试说明B点是否在暗礁区域外；(2)若继续向东航行，有无触礁危险?请说明理由．

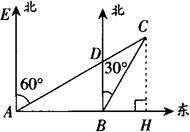
解 (1)∵AB=36×0．5=18，∠ADB=∠EAC=60°，∠DBC=30°，

∴∠ACB=30°．

又∵∠DAB=30°，

∴BC=AB=18>16．∴B点在暗礁区域外．

(2)过C作CH⊥AB，垂足为H．

在Rt△CAH中，∠CAH=30°．

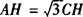∴，在Rt△CBH中，∠BCH=30°．

∴．

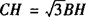设BH=x．∴．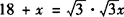

∴x=9．

∴．

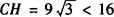∴船继续向东航行有触礁危险．

例14 “曙光中学”有一块三角形形状的花圃ABC，现可直接测量到∠A=30°，AC=40m，BC=25m，请你求出这块花圃的面积．

解 分两种情况计算：

当三角形为钝角三角形时，

过点C作CD⊥AB于D，

在Rt△ADC中，∠A=30°，AC=40，

∴CD=20，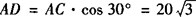

在Rt△CDB中，CD=20，CB=25，

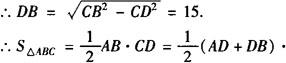
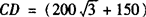(m²)．

(2)当三角形为锐角三角形时，过点C作CD⊥AB交AB的延长线于D，

由(1)可得CD=20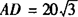，，DB=15．

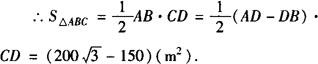
例15 如图，已知测速站P到公路L的距离PO为40m，一辆汽车在公路L上行驶，测得此车从点A行驶到点B所用的时间为2s，并测得∠APO=60°，∠BPO=30°，计算此车从A到B的平均速度为每秒多少米(结果保留四个有效数字)，并判断此车是否超过了22m/s的限制速度．

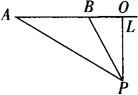
解 在Rt△BPO中，BO=OPtan30°，在Rt△APO中，AO=OPtan60°．

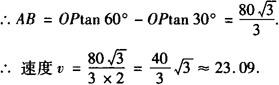
∴汽车超过了22m/s的限制速度．

例16 如图所示，某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处，经16小时的航行到达，到达后必须立即卸货，此时，接到气象部门通知，一台风中心正以40海里/时的速度由A向北偏西60°方向移动，距台风中心200海里的圆形区域(包括边界)均会受到影响．

(1)问：B处是否会受到台风的影响?请说明理由；

(2)为避免受到台风的影响，该船应在多少小时内卸完货物?

(供选用数据：，)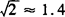

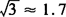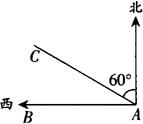
解 (1)过点B作BD⊥AC，垂足为D．

依题意得∠BAC=30°，在Rt△ABD中，BD=1/2AB=1/2×20×16=160<200．

∴B处会受到台风的影响．

(2)以点B为圆心，200海里为半径画圆交AC于E、F．(如图)

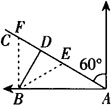
由勾股定理可求得DE=120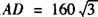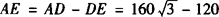，(海里)

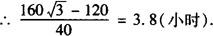
∴该船应在3．8小时内御完货物．