直线与双曲线

---

1．直线与双曲线的位置关系

它可以通过讨论双曲线方程与直线方程组成的方程组的实数解的个数来确定．通常是消去方程组中变量y(或x)得到关于变量x(或y)的一元二次方程．讨论△，则有

△>0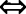直线和双曲线有两不同交点；

△=0直线和双曲线有且只有一个公共点；

△<0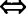直线和双曲线没有公共点．

直线与双曲线相交时，一定要注意直线与双曲线渐近线的关系：(α为一条渐近线倾斜角，θ为一直线倾斜角)

θ=α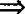只有一个交点，

θ>α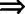有两个交点，

θ<α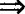有两个交点．

例1 一条直线交双曲线于A、B两点，交双曲线的渐近线于C、D两点，求证夹于渐近线和双曲线间的线段AC和BD相等．

证明 如图：

设双曲线方程为．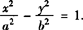

则其渐近线方程为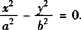．若直线与x轴平行，或与x轴垂直，根据双曲线的对称性结论显然成立．

若直线不与x轴平行且不与x轴垂直时，可设方程为y=kx+b(b≠0)代入双曲线方程整理得

(b²—a²k²)x²—2a²bkx—2a²b²=0．

设A(x₁，y₁)，B(x₂，y₂)，AB的中点为M(x₀，y₀)，则

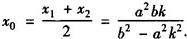
把直线方程代入渐近方程整理得：

(b²—a²k²)x²—2a²bkx—a²b²=0．

设C(x₃，y₃)、D(x₄，y₄)，CD的中点为N(x₀′，y₀′)，

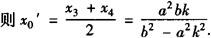
而M、N都在直线上，于是M、N重合，即线段AB的中点与线段CD的中点重合，故|AC|=|BD|．

2．焦点弦问题

例2 过双曲线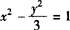的左焦点F₁作倾斜角为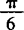的弦AB，求

❶ |AB|；
❷ △F₂AB的周长(F₂为双曲线的右焦点)．

解(1) 方法一 双曲线焦点F₁(—2，0)，F₂(2，0)，直线AB方程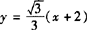代入双曲线方程，得

8x²—4x—13=0．

设A(x₁，y₁)，B(x₂，y₂)

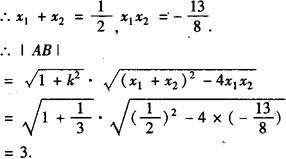
方法二 根据双曲线的第二定义得：

|BF₁|=a+ex₂=1+2x₂，

|AF₁|=—(a+ex₁)=—1—2x₁．

∴|AB|=|BF₁|—|AF₁|

=1+2x₂—(—1—2x₁)

=2+2(x₁+x₂)

=2+2×1/2=3．

(2)由双曲线第二定义得

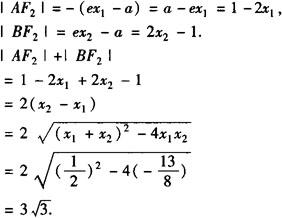
∴△F₂AB的周长为．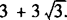

3．中点弦问题

例3 已知双曲线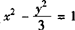上存在关于直线l∶y=kx+4的对称点，如图，求实数k的取值范围，并求中点M的轨迹．

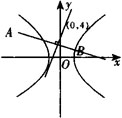
策略 本题解题的关键是合理利用几何条件“垂直”和“平分”且满足于△>0成立．

解 当k=0时，显然不成立．

所以当k≠0时，由l⊥AB，可设直线AB的方程为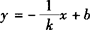将其代入3x²—y²=3中：得(3k²—1)x²+2kbx—(b²+3)k²=0显然3k²—1≠0，且△>0，即k²b²+3k²—1>0， ❶ 

由韦达定理得M的坐标为

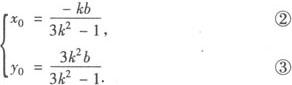
因为l平分AB，故M(x₀，y₀)在直线l上，从而有，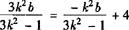

即k²b=3k²—1．❹ 

将❹ 代入❶ 得：k²b²+k²b>0，所以b>0或b<—1．

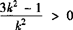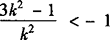故或，所以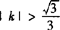或|k|<1/2且k≠0．

将❹ 代入❷ 、❸ 得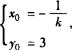，即M中点轨迹为y₀=3(|x₀|>2或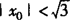且x₀≠0)．

综上所述，当k∈(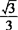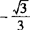，+∞)∪(—∞，)∪(—1/2，0)∪(0，1/2)时，双曲线存在一条弦被直线l垂直平分，且弦中点的轨迹方程为y=3(|x|>2或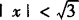且x≠0)．