点估计法

---

点估计分为参数点估计与非参数点估计两类。

在参数点估计中，设总体的分布类型是已知的，仅有有限个未知的参数，记作θ(可以是向量)。设x₁，…，x_n是来自总体的容量为n的样本。点估计问题就是要构造一个统计量T(x₁，…，x_n)作为θ的已知函数g(θ)的估计量，使得当我们得到了样本x₁，…，x_n的观察值(x₁，…，x_n)时，便可以计算出T(x₁，…，x_n)，作为g(θ)的估计值。

非参数点估计与参数点估计的不同之处在于，对总体的分布类型不事先做出假定，目的仍然是通过样本来估计总体的某种特性。

比如要估计总体的均值、方差、容许限(to1erance 1imits)等。

参数点估计常用的估计方法有矩估计法、极大似然估计法、最小二聚法、贝叶斯方法等(见各有关条目)。

非参数点估计常常利用顺序统计量。例如，如果要估计总体分布的p分位数，在总体分布类型未知的情形下，样本p分位数就是一个较好的估计量。

对于同一个估计问题，可以有一个以上的估计量。这样，在估计量之间就存在著优劣问题。

例如，设总体服从(0₁，θ₂)上的均匀分布，θ_i，i=1，2，是未知参数，x₁，…，x_n为来自该总体的独立随机样本。显然总体的数学期望为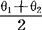，它的矩估计为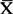，而它的极大似然估计则为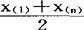，其中x₍₁₎=min｛x₁，…，x_n｝，x_(n)=max｛x₁，…，x_n｝。

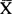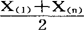在数理统计中提出了若干准则来评定估计量的优劣。如无偏性、最小方差性、相合性、不变性、可容许性、渐近正态性、稳健性等。前例中的两个估计量与同为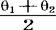的无偏估计，但在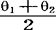的所有无偏估计中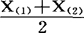，的方差最小，即它是最小方差无偏估计，而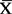则不是。